NOTE
이 문서는 양자 정보와 계산 복습 문제 풀이를 위한 문서입니다.
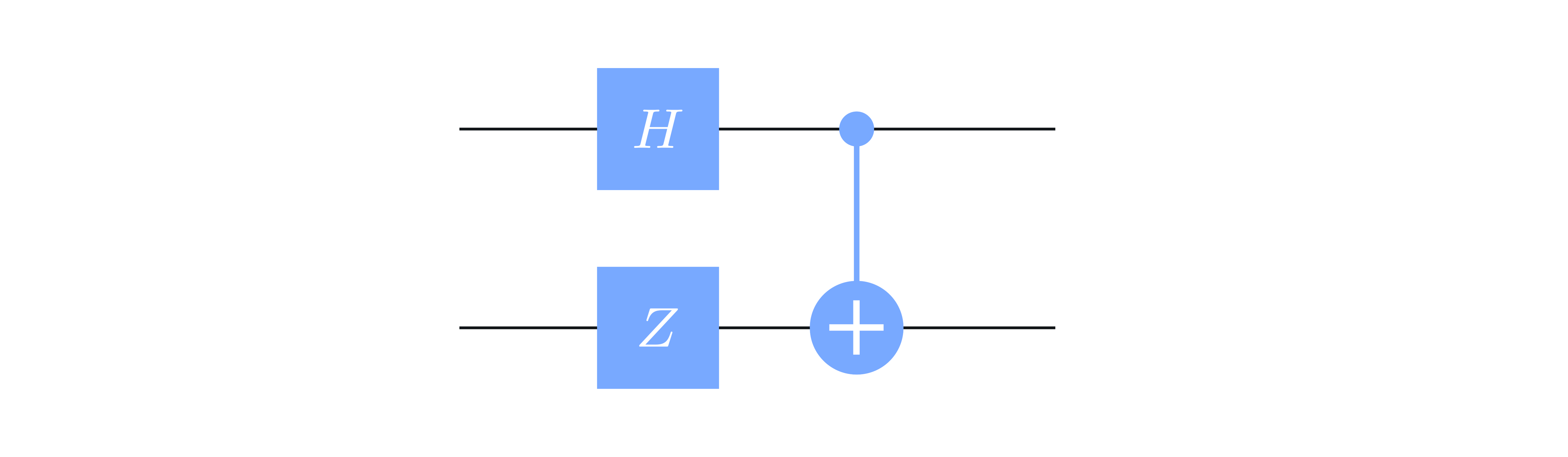
다음 양자 회로는 어떤 Bell 상태를 생성하는가? 각 qubit은 표준적으로 ∣ 0 ⟩ |0\rangle ∣0 ⟩
회로 구성:
Qubit 0 (상단 선) : Hadamard 게이트(H) → CNOT의 제어(control) qubitQubit 1 (하단 선) : Pauli-Z 게이트(Z) → CNOT의 대상(target) qubitCNOT 게이트 : Qubit 0이 제어, Qubit 1이 대상양자 상태는 복소수 계수를 가진 벡터로 표현됩니다 정규화 조건: 계수들의 절댓값 제곱의 합이 1이어야 합니다 두 qubit 시스템의 상태는 ∣ a b ⟩ |ab\rangle ∣ ab ⟩ a , b ∈ { 0 , 1 } a, b \in \{0,1\} a , b ∈ { 0 , 1 } 행렬 표현:H = 1 2 ( 1 1 1 − 1 ) H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} H = 2 1 ( 1 1 1 − 1 )
동작:H ∣ 0 ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = ∣ + ⟩ H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = |+\rangle H ∣0 ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) = ∣ + ⟩
H ∣ 1 ⟩ = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) = ∣ − ⟩ H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = |-\rangle H ∣1 ⟩ = 2 1 ( ∣0 ⟩ − ∣1 ⟩) = ∣ − ⟩
Hadamard 게이트는 표준 기저 상태를 중첩 상태로 변환합니다 행렬 표현:Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 )
동작:Z ∣ 0 ⟩ = ∣ 0 ⟩ , Z ∣ 1 ⟩ = − ∣ 1 ⟩ Z|0\rangle = |0\rangle, \quad Z|1\rangle = -|1\rangle Z ∣0 ⟩ = ∣0 ⟩ , Z ∣1 ⟩ = − ∣1 ⟩
Pauli-Z 게이트는 위상 플립(phase flip) 연산으로, ∣ 1 ⟩ |1\rangle ∣1 ⟩ 제어 qubit이 ∣ 0 ⟩ |0\rangle ∣0 ⟩ 제어 qubit이 ∣ 1 ⟩ |1\rangle ∣1 ⟩ 행렬 표현 (첫 번째 qubit이 제어인 경우):CNOT = ( 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ) \text{CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} CNOT = 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
표준 기저 상태에 대한 동작:∣ 00 ⟩ ↦ ∣ 00 ⟩ , ∣ 01 ⟩ ↦ ∣ 01 ⟩ |00\rangle \mapsto |00\rangle, \quad |01\rangle \mapsto |01\rangle ∣00 ⟩ ↦ ∣00 ⟩ , ∣01 ⟩ ↦ ∣01 ⟩
∣ 10 ⟩ ↦ ∣ 11 ⟩ , ∣ 11 ⟩ ↦ ∣ 10 ⟩ |10\rangle \mapsto |11\rangle, \quad |11\rangle \mapsto |10\rangle ∣10 ⟩ ↦ ∣11 ⟩ , ∣11 ⟩ ↦ ∣10 ⟩
Bell 상태는 두 qubit의 최대 얽힘 상태입니다:
∣ ϕ + ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) ∣ ϕ + ⟩ = 2 1 ( ∣00 ⟩ + ∣11 ⟩) ∣ ϕ − ⟩ = 1 2 ( ∣ 00 ⟩ − ∣ 11 ⟩ ) |\phi^-\rangle = \frac{1}{\sqrt{2}}(|00\rangle - |11\rangle) ∣ ϕ − ⟩ = 2 1 ( ∣00 ⟩ − ∣11 ⟩) ∣ ψ + ⟩ = 1 2 ( ∣ 01 ⟩ + ∣ 10 ⟩ ) |\psi^+\rangle = \frac{1}{\sqrt{2}}(|01\rangle + |10\rangle) ∣ ψ + ⟩ = 2 1 ( ∣01 ⟩ + ∣10 ⟩) ∣ ψ − ⟩ = 1 2 ( ∣ 01 ⟩ − ∣ 10 ⟩ ) |\psi^-\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |10\rangle) ∣ ψ − ⟩ = 2 1 ( ∣01 ⟩ − ∣10 ⟩) 양자 회로에서 게이트는 왼쪽에서 오른쪽으로 순차적으로 적용됩니다 동시에 적용되는 게이트는 병렬로 작동합니다 텐서 곱을 사용하여 다중 qubit 시스템에 단일 qubit 게이트를 적용할 수 있습니다 두 qubit이 모두 ∣ 0 ⟩ |0\rangle ∣0 ⟩
∣ ψ 0 ⟩ = ∣ 00 ⟩ |\psi_0\rangle = |00\rangle ∣ ψ 0 ⟩ = ∣00 ⟩
Qubit 0에 Hadamard 게이트를 적용합니다. 이는 H ⊗ I H \otimes \mathbb{I} H ⊗ I
∣ ψ 1 ⟩ = ( H ⊗ I ) ∣ 00 ⟩ = H ∣ 0 ⟩ ⊗ ∣ 0 ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ ∣ 0 ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 10 ⟩ \begin{aligned} |\psi_1\rangle &= (H \otimes \mathbb{I})|00\rangle \\ &= H|0\rangle \otimes |0\rangle \\ &= \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes |0\rangle \\ &= \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|10\rangle \end{aligned} ∣ ψ 1 ⟩ = ( H ⊗ I ) ∣00 ⟩ = H ∣0 ⟩ ⊗ ∣0 ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) ⊗ ∣0 ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣10 ⟩
Qubit 1에 Pauli-Z 게이트를 적용합니다. 이는 I ⊗ Z \mathbb{I} \otimes Z I ⊗ Z
∣ ψ 2 ⟩ = ( I ⊗ Z ) ∣ ψ 1 ⟩ = ( I ⊗ Z ) ( 1 2 ∣ 00 ⟩ + 1 2 ∣ 10 ⟩ ) = 1 2 ( I ⊗ Z ) ∣ 00 ⟩ + 1 2 ( I ⊗ Z ) ∣ 10 ⟩ = 1 2 ∣ 0 ⟩ ⊗ Z ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ ⊗ Z ∣ 0 ⟩ = 1 2 ∣ 0 ⟩ ⊗ ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ ⊗ ∣ 0 ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 10 ⟩ \begin{aligned} |\psi_2\rangle &= (\mathbb{I} \otimes Z)|\psi_1\rangle \\ &= (\mathbb{I} \otimes Z)\left(\frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|10\rangle\right) \\ &= \frac{1}{\sqrt{2}}(\mathbb{I} \otimes Z)|00\rangle + \frac{1}{\sqrt{2}}(\mathbb{I} \otimes Z)|10\rangle \\ &= \frac{1}{\sqrt{2}}|0\rangle \otimes Z|0\rangle + \frac{1}{\sqrt{2}}|1\rangle \otimes Z|0\rangle \\ &= \frac{1}{\sqrt{2}}|0\rangle \otimes |0\rangle + \frac{1}{\sqrt{2}}|1\rangle \otimes |0\rangle \\ &= \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|10\rangle \end{aligned} ∣ ψ 2 ⟩ = ( I ⊗ Z ) ∣ ψ 1 ⟩ = ( I ⊗ Z ) ( 2 1 ∣00 ⟩ + 2 1 ∣10 ⟩ ) = 2 1 ( I ⊗ Z ) ∣00 ⟩ + 2 1 ( I ⊗ Z ) ∣10 ⟩ = 2 1 ∣0 ⟩ ⊗ Z ∣0 ⟩ + 2 1 ∣1 ⟩ ⊗ Z ∣0 ⟩ = 2 1 ∣0 ⟩ ⊗ ∣0 ⟩ + 2 1 ∣1 ⟩ ⊗ ∣0 ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣10 ⟩
참고 : Z ∣ 0 ⟩ = ∣ 0 ⟩ Z|0\rangle = |0\rangle Z ∣0 ⟩ = ∣0 ⟩
CNOT 게이트를 적용합니다 (Qubit 0이 제어, Qubit 1이 대상):
∣ ψ 3 ⟩ = CNOT ∣ ψ 2 ⟩ = CNOT ( 1 2 ∣ 00 ⟩ + 1 2 ∣ 10 ⟩ ) = 1 2 CNOT ∣ 00 ⟩ + 1 2 CNOT ∣ 10 ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ \begin{aligned} |\psi_3\rangle &= \text{CNOT}|\psi_2\rangle \\ &= \text{CNOT}\left(\frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|10\rangle\right) \\ &= \frac{1}{\sqrt{2}}\text{CNOT}|00\rangle + \frac{1}{\sqrt{2}}\text{CNOT}|10\rangle \\ &= \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle \end{aligned} ∣ ψ 3 ⟩ = CNOT ∣ ψ 2 ⟩ = CNOT ( 2 1 ∣00 ⟩ + 2 1 ∣10 ⟩ ) = 2 1 CNOT ∣00 ⟩ + 2 1 CNOT ∣10 ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩
여기서:
CNOT ∣ 00 ⟩ = ∣ 00 ⟩ \text{CNOT}|00\rangle = |00\rangle CNOT ∣00 ⟩ = ∣00 ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ CNOT ∣ 10 ⟩ = ∣ 11 ⟩ \text{CNOT}|10\rangle = |11\rangle CNOT ∣10 ⟩ = ∣11 ⟩ ∣ 1 ⟩ |1\rangle ∣1 ⟩ ∣ ψ 3 ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ = ∣ ϕ + ⟩ |\psi_3\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle = |\phi^+\rangle ∣ ψ 3 ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩ = ∣ ϕ + ⟩
결과: ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩
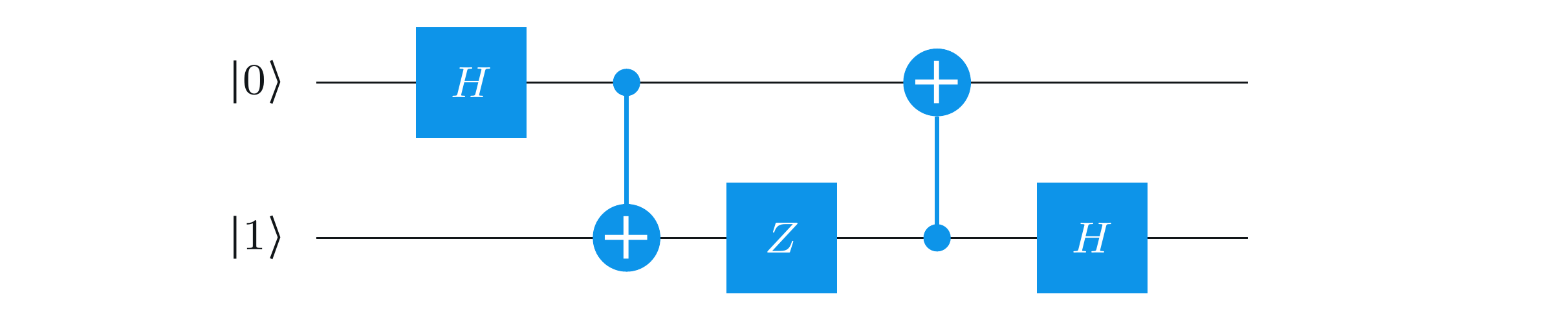
다음 두 qubit 양자 회로의 출력 상태를 계산하라. Qiskit 순서(little-endian) 규약을 따르며, 상태는 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩
회로 구성:
Qubit 0 (상단 선) : 초기 상태 ∣ 0 ⟩ |0\rangle ∣0 ⟩ Qubit 1 (하단 선) : 초기 상태 ∣ 1 ⟩ |1\rangle ∣1 ⟩ 연산 순서:
Qubit 0에 Hadamard 게이트 적용 첫 번째 CNOT 게이트 (Qubit 0이 제어, Qubit 1이 대상) Qubit 1에 Pauli-Z 게이트 적용 두 번째 CNOT 게이트 (Qubit 1이 제어, Qubit 0이 대상) Qubit 1에 Hadamard 게이트 적용 Qiskit에서는 상태를 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩ 위 선이 q₀, 아래 선이 q₁에 해당합니다 초기 상태가 다를 수 있으므로 회로 다이어그램을 주의 깊게 확인해야 합니다 중요 : 문제를 풀 때마다 "이 문제는 Qiskit ordering인가?" 를 먼저 체크하고, 회로 해석 전에 초기 상태를 명시적으로 적어야 합니다H ∣ 0 ⟩ = ∣ + ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) H|0\rangle = |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) H ∣0 ⟩ = ∣ + ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) H ∣ 1 ⟩ = ∣ − ⟩ = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) H|1\rangle = |-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) H ∣1 ⟩ = ∣ − ⟩ = 2 1 ( ∣0 ⟩ − ∣1 ⟩) H ∣ + ⟩ = ∣ 0 ⟩ H|+\rangle = |0\rangle H ∣ + ⟩ = ∣0 ⟩ H ∣ − ⟩ = ∣ 1 ⟩ H|-\rangle = |1\rangle H ∣ − ⟩ = ∣1 ⟩ 중요 : Hadamard 작용을 상태별로 정확히 암기해야 합니다 (조건 반사 수준)CNOT 뒤에 H가 나오면 간섭(interference) 발생 여부를 점검해야 합니다 Z ∣ 0 ⟩ = ∣ 0 ⟩ Z|0\rangle = |0\rangle Z ∣0 ⟩ = ∣0 ⟩ Z ∣ 1 ⟩ = − ∣ 1 ⟩ Z|1\rangle = -|1\rangle Z ∣1 ⟩ = − ∣1 ⟩ 위상 플립 연산으로, ∣ 1 ⟩ |1\rangle ∣1 ⟩ 중요 : 위상(phase) 처리를 정확히 해야 합니다. 부호 하나라도 있으면 끝까지 추적 해야 합니다Global phase는 무시하지만, **상대 위상(relative phase)**은 결과를 바꿉니다 CNOT 게이트는 제어 qubit과 대상 qubit의 역할이 중요합니다 제어 qubit이 ∣ 1 ⟩ |1\rangle ∣1 ⟩ 회로에서 제어와 대상의 위치를 정확히 파악해야 합니다 Qiskit 순서 규약에 따라 상태를 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩
Qubit 0 (상단 선): ∣ 0 ⟩ |0\rangle ∣0 ⟩ Qubit 1 (하단 선): ∣ 1 ⟩ |1\rangle ∣1 ⟩ 따라서 초기 상태는:
∣ ψ 0 ⟩ = ∣ 10 ⟩ ( 즉, ∣ q 1 = 1 , q 0 = 0 ⟩ ) |\psi_0\rangle = |10\rangle \quad (\text{즉, } |q_1=1, q_0=0\rangle) ∣ ψ 0 ⟩ = ∣10 ⟩ ( 즉 , ∣ q 1 = 1 , q 0 = 0 ⟩)
Qubit 0에 Hadamard 게이트를 적용합니다:
H ∣ 0 ⟩ = ∣ + ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ∣ ψ 1 ⟩ = 1 2 ∣ 10 ⟩ + 1 2 ∣ 11 ⟩ \begin{aligned} H|0\rangle &= |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\ |\psi_1\rangle &= \frac{1}{\sqrt{2}}|10\rangle + \frac{1}{\sqrt{2}}|11\rangle \end{aligned} H ∣0 ⟩ ∣ ψ 1 ⟩ = ∣ + ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) = 2 1 ∣10 ⟩ + 2 1 ∣11 ⟩
CNOT 게이트를 적용합니다 (Qubit 0이 제어, Qubit 1이 대상):
∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ ∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩ ∣ 1 ⟩ |1\rangle ∣1 ⟩ ∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ ψ 2 ⟩ = 1 2 ∣ 10 ⟩ + 1 2 ∣ 01 ⟩ = 1 2 ∣ 01 ⟩ + 1 2 ∣ 10 ⟩ \begin{aligned} |\psi_2\rangle &= \frac{1}{\sqrt{2}}|10\rangle + \frac{1}{\sqrt{2}}|01\rangle \\ &= \frac{1}{\sqrt{2}}|01\rangle + \frac{1}{\sqrt{2}}|10\rangle \end{aligned} ∣ ψ 2 ⟩ = 2 1 ∣10 ⟩ + 2 1 ∣01 ⟩ = 2 1 ∣01 ⟩ + 2 1 ∣10 ⟩
Qubit 1에 Pauli-Z 게이트를 적용합니다. 위상(phase) 처리를 정확히 추적 해야 합니다:
∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ Z ∣ 0 ⟩ = ∣ 0 ⟩ Z|0\rangle = |0\rangle Z ∣0 ⟩ = ∣0 ⟩ ∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ 1 ⟩ |1\rangle ∣1 ⟩ Z ∣ 1 ⟩ = − ∣ 1 ⟩ Z|1\rangle = -|1\rangle Z ∣1 ⟩ = − ∣1 ⟩ − ∣ 10 ⟩ -|10\rangle − ∣10 ⟩ 위상 반전 )위상 추적 주의 : Z Z Z ∣ 1 ⟩ |1\rangle ∣1 ⟩ − 1 -1 − 1
∣ ψ 3 ⟩ = 1 2 ∣ 01 ⟩ − 1 2 ∣ 10 ⟩ \begin{aligned} |\psi_3\rangle &= \frac{1}{\sqrt{2}}|01\rangle - \frac{1}{\sqrt{2}}|10\rangle \end{aligned} ∣ ψ 3 ⟩ = 2 1 ∣01 ⟩ − 2 1 ∣10 ⟩
중요 : Global phase는 무시하지만, 여기서는 두 항의 상대 위상 차이 가 있으므로 이 부호를 끝까지 추적해야 합니다.
두 번째 CNOT 게이트를 적용합니다 (Qubit 1이 제어, Qubit 0이 대상):
∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ ∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ 1 ⟩ |1\rangle ∣1 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩ ∣ ψ 4 ⟩ = 1 2 ∣ 01 ⟩ − 1 2 ∣ 11 ⟩ \begin{aligned} |\psi_4\rangle &= \frac{1}{\sqrt{2}}|01\rangle - \frac{1}{\sqrt{2}}|11\rangle \end{aligned} ∣ ψ 4 ⟩ = 2 1 ∣01 ⟩ − 2 1 ∣11 ⟩
Qubit 1에 Hadamard 게이트를 적용합니다. ∣ ψ 4 ⟩ = 1 2 ∣ 01 ⟩ − 1 2 ∣ 11 ⟩ |\psi_4\rangle = \frac{1}{\sqrt{2}}|01\rangle - \frac{1}{\sqrt{2}}|11\rangle ∣ ψ 4 ⟩ = 2 1 ∣01 ⟩ − 2 1 ∣11 ⟩
Hadamard 게이트의 정확한 작용 (조건 반사 수준으로 암기):
H ∣ 0 ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = ∣ + ⟩ H ∣ 1 ⟩ = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) = ∣ − ⟩ \begin{aligned} H|0\rangle &= \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = |+\rangle \\ H|1\rangle &= \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = |-\rangle \end{aligned} H ∣0 ⟩ H ∣1 ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) = ∣ + ⟩ = 2 1 ( ∣0 ⟩ − ∣1 ⟩) = ∣ − ⟩
각 항에 적용 (Qiskit 순서 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩
∣ 01 ⟩ = ∣ q 1 = 0 , q 0 = 1 ⟩ |01\rangle = |q_1=0, q_0=1\rangle ∣01 ⟩ = ∣ q 1 = 0 , q 0 = 1 ⟩ H ∣ 0 ⟩ ⊗ ∣ 1 ⟩ = ∣ + ⟩ ⊗ ∣ 1 ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ ∣ 1 ⟩ = 1 2 ( ∣ 01 ⟩ + ∣ 11 ⟩ ) H|0\rangle \otimes |1\rangle = |+\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes |1\rangle = \frac{1}{\sqrt{2}}(|01\rangle + |11\rangle) H ∣0 ⟩ ⊗ ∣1 ⟩ = ∣ + ⟩ ⊗ ∣1 ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) ⊗ ∣1 ⟩ = 2 1 ( ∣01 ⟩ + ∣11 ⟩) ∣ 11 ⟩ = ∣ q 1 = 1 , q 0 = 1 ⟩ |11\rangle = |q_1=1, q_0=1\rangle ∣11 ⟩ = ∣ q 1 = 1 , q 0 = 1 ⟩ H ∣ 1 ⟩ ⊗ ∣ 1 ⟩ = ∣ − ⟩ ⊗ ∣ 1 ⟩ = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) ⊗ ∣ 1 ⟩ = 1 2 ( ∣ 01 ⟩ − ∣ 11 ⟩ ) H|1\rangle \otimes |1\rangle = |-\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) \otimes |1\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |11\rangle) H ∣1 ⟩ ⊗ ∣1 ⟩ = ∣ − ⟩ ⊗ ∣1 ⟩ = 2 1 ( ∣0 ⟩ − ∣1 ⟩) ⊗ ∣1 ⟩ = 2 1 ( ∣01 ⟩ − ∣11 ⟩) 위상 추적 주의 : 두 번째 항의 계수가 − 1 2 -\frac{1}{\sqrt{2}} − 2 1
∣ ψ 5 ⟩ = 1 2 ⋅ 1 2 ( ∣ 01 ⟩ + ∣ 11 ⟩ ) − 1 2 ⋅ 1 2 ( ∣ 01 ⟩ − ∣ 11 ⟩ ) = 1 2 ∣ 01 ⟩ + 1 2 ∣ 11 ⟩ − 1 2 ∣ 01 ⟩ + 1 2 ∣ 11 ⟩ = 1 2 ∣ 01 ⟩ − 1 2 ∣ 01 ⟩ + 1 2 ∣ 11 ⟩ + 1 2 ∣ 11 ⟩ = 0 ⋅ ∣ 01 ⟩ + ∣ 11 ⟩ = ∣ 11 ⟩ \begin{aligned} |\psi_5\rangle &= \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}}(|01\rangle + |11\rangle) - \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}}(|01\rangle - |11\rangle) \\ &= \frac{1}{2}|01\rangle + \frac{1}{2}|11\rangle - \frac{1}{2}|01\rangle + \frac{1}{2}|11\rangle \\ &= \frac{1}{2}|01\rangle - \frac{1}{2}|01\rangle + \frac{1}{2}|11\rangle + \frac{1}{2}|11\rangle \\ &= 0 \cdot |01\rangle + |11\rangle \\ &= |11\rangle \end{aligned} ∣ ψ 5 ⟩ = 2 1 ⋅ 2 1 ( ∣01 ⟩ + ∣11 ⟩) − 2 1 ⋅ 2 1 ( ∣01 ⟩ − ∣11 ⟩) = 2 1 ∣01 ⟩ + 2 1 ∣11 ⟩ − 2 1 ∣01 ⟩ + 2 1 ∣11 ⟩ = 2 1 ∣01 ⟩ − 2 1 ∣01 ⟩ + 2 1 ∣11 ⟩ + 2 1 ∣11 ⟩ = 0 ⋅ ∣01 ⟩ + ∣11 ⟩ = ∣11 ⟩
간섭(interference) 발생 : ∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩
∣ ψ 5 ⟩ = ∣ 11 ⟩ |\psi_5\rangle = |11\rangle ∣ ψ 5 ⟩ = ∣11 ⟩
결과: 최종 출력 상태는 ∣ 11 ⟩ |11\rangle ∣11 ⟩
다음 행렬 M M M
M = ( 1 0 0 − 1 ) M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} M = ( 1 0 0 − 1 )
정의: M † = M M^\dagger = M M † = M M † M^\dagger M † M M M 실수 행렬의 경우, 전치 행렬 M T M^T M T Hermitian 행렬의 고유값은 모두 실수입니다 정의: U † U = I U^\dagger U = I U † U = I U U † = I UU^\dagger = I U U † = I 유니터리 행렬은 역행렬이 존재하며, U − 1 = U † U^{-1} = U^\dagger U − 1 = U † 유니터리 연산은 양자 상태의 확률을 보존합니다 (정규화 조건 유지) 모든 Pauli 행렬(X, Y, Z)은 유니터리입니다 정의: P 2 = P P^2 = P P 2 = P P † = P P^\dagger = P P † = P Projection 행렬은 자기 자신을 제곱하면 자기 자신이 됩니다 고유값은 0 또는 1만 가질 수 있습니다 정의: 다음 두 조건을 만족하는 행렬 모든 항목은 음이 아닌 실수입니다 (M i j ≥ 0 M_{ij} \geq 0 M ij ≥ 0 모든 열의 항목들의 합은 1입니다 (∑ i M i j = 1 \sum_i M_{ij} = 1 ∑ i M ij = 1 확률 벡터를 확률 벡터로 매핑합니다 주어진 행렬 M = ( 1 0 0 − 1 ) M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} M = ( 1 0 0 − 1 )
Z ∣ 0 ⟩ = ∣ 0 ⟩ Z|0\rangle = |0\rangle Z ∣0 ⟩ = ∣0 ⟩ Z ∣ 1 ⟩ = − ∣ 1 ⟩ Z|1\rangle = -|1\rangle Z ∣1 ⟩ = − ∣1 ⟩ 주어진 행렬:
M = ( 1 0 0 − 1 ) M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} M = ( 1 0 0 − 1 )
M M M M † = M T M^\dagger = M^T M † = M T
M T = ( 1 0 0 − 1 ) = M M^T = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = M M T = ( 1 0 0 − 1 ) = M
따라서 M † = M M^\dagger = M M † = M Hermitian입니다 .
M † M M^\dagger M M † M
M † M = M T M ( 실수 행렬이므로 ) = ( 1 0 0 − 1 ) ( 1 0 0 − 1 ) = ( 1 ⋅ 1 + 0 ⋅ 0 1 ⋅ 0 + 0 ⋅ ( − 1 ) 0 ⋅ 1 + ( − 1 ) ⋅ 0 0 ⋅ 0 + ( − 1 ) ⋅ ( − 1 ) ) = ( 1 0 0 1 ) = I \begin{aligned} M^\dagger M &= M^T M \quad (\text{실수 행렬이므로}) \\ &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \\ &= \begin{pmatrix} 1 \cdot 1 + 0 \cdot 0 & 1 \cdot 0 + 0 \cdot (-1) \\ 0 \cdot 1 + (-1) \cdot 0 & 0 \cdot 0 + (-1) \cdot (-1) \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = I \end{aligned} M † M = M T M ( 실수 행렬이므로 ) = ( 1 0 0 − 1 ) ( 1 0 0 − 1 ) = ( 1 ⋅ 1 + 0 ⋅ 0 0 ⋅ 1 + ( − 1 ) ⋅ 0 1 ⋅ 0 + 0 ⋅ ( − 1 ) 0 ⋅ 0 + ( − 1 ) ⋅ ( − 1 ) ) = ( 1 0 0 1 ) = I
따라서 M † M = I M^\dagger M = I M † M = I Unitary입니다 .
M 2 M^2 M 2
M 2 = ( 1 0 0 − 1 ) ( 1 0 0 − 1 ) = ( 1 0 0 1 ) = I ≠ M \begin{aligned} M^2 &= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = I \neq M \end{aligned} M 2 = ( 1 0 0 − 1 ) ( 1 0 0 − 1 ) = ( 1 0 0 1 ) = I = M
M 2 = I ≠ M M^2 = I \neq M M 2 = I = M Projection이 아닙니다 .
Stochastic 행렬의 조건:
모든 항목이 음이 아닌 실수여야 함 모든 열의 합이 1이어야 함 M M M 0 + ( − 1 ) = − 1 ≠ 1 0 + (-1) = -1 \neq 1 0 + ( − 1 ) = − 1 = 1
또한 두 번째 열에 음수(− 1 -1 − 1 Stochastic이 아닙니다 .
결과: M M M
M M M
다음 두 qubit 양자 회로의 유니터리 행렬을 계산하라. Qiskit 규약을 따라 qubit 순서를 사용한다.
회로 구성:
Qubit 0 (상단 선) : Pauli-X 게이트(X) → CNOT의 제어(control) → Hadamard 게이트(H)Qubit 1 (하단 선) : Phase 게이트(S) → CNOT의 대상(target) → Hadamard 게이트(H)연산 순서:
Qubit 0에 X, Qubit 1에 S (병렬 적용) CNOT 게이트 (Qubit 0이 제어, Qubit 1이 대상) Qubit 0에 H, Qubit 1에 H (병렬 적용) Qiskit에서는 상태를 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩ 병렬로 적용되는 게이트는 텐서 곱으로 표현됩니다 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩ U U U V V V U ⊗ V U \otimes V U ⊗ V 두 행렬 A = ( a b c d ) A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} A = ( a c b d ) B = ( e f g h ) B = \begin{pmatrix} e & f \\ g & h \end{pmatrix} B = ( e g f h )
A ⊗ B = ( a B b B c B d B ) = ( a e a f b e b f a g a h b g b h c e c f d e d f c g c h d g d h ) A \otimes B = \begin{pmatrix} aB & bB \\ cB & dB \end{pmatrix} = \begin{pmatrix} ae & af & be & bf \\ ag & ah & bg & bh \\ ce & cf & de & df \\ cg & ch & dg & dh \end{pmatrix} A ⊗ B = ( a B c B b B d B ) = a e a g ce c g a f ah c f c h b e b g d e d g b f bh df d h
양자 회로의 전체 유니터리 행렬은 각 레이어의 행렬을 오른쪽에서 왼쪽으로 곱한 것입니다 U = U final ⋅ U middle ⋅ U initial U = U_{\text{final}} \cdot U_{\text{middle}} \cdot U_{\text{initial}} U = U final ⋅ U middle ⋅ U initial Qiskit 순서 확인 : ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩
텐서 곱 순서 : Qiskit 순서에서 Qubit 1에 S S S X X X S ⊗ X S \otimes X S ⊗ X
Qubit 1 (아래 선)에 S S S Qubit 0 (위 선)에 X X X S ⊗ X = ( 1 0 0 i ) ⊗ ( 0 1 1 0 ) = ( 1 ⋅ ( 0 1 1 0 ) 0 ⋅ ( 0 1 1 0 ) 0 ⋅ ( 0 1 1 0 ) i ⋅ ( 0 1 1 0 ) ) = ( 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0 ) \begin{aligned} S \otimes X &= \begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix} \otimes \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \\ &= \begin{pmatrix} 1 \cdot \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} & 0 \cdot \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \\ 0 \cdot \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} & i \cdot \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{pmatrix} \\ &= \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i \\ 0 & 0 & i & 0 \end{pmatrix} \end{aligned} S ⊗ X = ( 1 0 0 i ) ⊗ ( 0 1 1 0 ) = 1 ⋅ ( 0 1 1 0 ) 0 ⋅ ( 0 1 1 0 ) 0 ⋅ ( 0 1 1 0 ) i ⋅ ( 0 1 1 0 ) = 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0
U 1 = ( 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0 ) U_1 = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i \\ 0 & 0 & i & 0 \end{pmatrix} U 1 = 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0
CNOT 게이트 (q₀이 제어, q₁이 대상):
U 2 = CNOT 01 = ( 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ) U_2 = \text{CNOT}_{01} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} U 2 = CNOT 01 = 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0
Qubit 0과 Qubit 1 모두에 Hadamard 게이트를 병렬 적용:
H ⊗ H = 1 2 ( 1 1 1 − 1 ) ⊗ 1 2 ( 1 1 1 − 1 ) = 1 2 ( 1 ⋅ ( 1 1 1 − 1 ) 1 ⋅ ( 1 1 1 − 1 ) 1 ⋅ ( 1 1 1 − 1 ) − 1 ⋅ ( 1 1 1 − 1 ) ) = 1 2 ( 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ) \begin{aligned} H \otimes H &= \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \otimes \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \\ &= \frac{1}{2} \begin{pmatrix} 1 \cdot \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} & 1 \cdot \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \\ 1 \cdot \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} & -1 \cdot \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \end{pmatrix} \\ &= \frac{1}{2} \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{pmatrix} \end{aligned} H ⊗ H = 2 1 ( 1 1 1 − 1 ) ⊗ 2 1 ( 1 1 1 − 1 ) = 2 1 1 ⋅ ( 1 1 1 − 1 ) 1 ⋅ ( 1 1 1 − 1 ) 1 ⋅ ( 1 1 1 − 1 ) − 1 ⋅ ( 1 1 1 − 1 ) = 2 1 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1
U 3 = 1 2 ( 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ) U_3 = \frac{1}{2} \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{pmatrix} U 3 = 2 1 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1
전체 유니터리 행렬은 U = U 3 ⋅ U 2 ⋅ U 1 U = U_3 \cdot U_2 \cdot U_1 U = U 3 ⋅ U 2 ⋅ U 1
먼저 U 2 ⋅ U 1 U_2 \cdot U_1 U 2 ⋅ U 1
U 2 U 1 = ( 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ) ( 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0 ) = ( 0 1 0 0 0 0 i 0 0 0 0 i 1 0 0 0 ) \begin{aligned} U_2 U_1 &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i \\ 0 & 0 & i & 0 \end{pmatrix} \\ &= \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & 0 & 0 & i \\ 1 & 0 & 0 & 0 \end{pmatrix} \end{aligned} U 2 U 1 = 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 i 0 0 i 0 = 0 0 0 1 1 0 0 0 0 i 0 0 0 0 i 0
다음으로 U 3 ⋅ ( U 2 U 1 ) U_3 \cdot (U_2 U_1) U 3 ⋅ ( U 2 U 1 )
U = U 3 ⋅ ( U 2 U 1 ) = 1 2 ( 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ) ( 0 1 0 0 0 0 i 0 0 0 0 i 1 0 0 0 ) = 1 2 ( 1 1 i i − 1 1 − i i − 1 1 i − i 1 1 − i − i ) \begin{aligned} U &= U_3 \cdot (U_2 U_1) \\ &= \frac{1}{2} \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & 0 & 0 & i \\ 1 & 0 & 0 & 0 \end{pmatrix} \\ &= \frac{1}{2} \begin{pmatrix} 1 & 1 & i & i \\ -1 & 1 & -i & i \\ -1 & 1 & i & -i \\ 1 & 1 & -i & -i \end{pmatrix} \end{aligned} U = U 3 ⋅ ( U 2 U 1 ) = 2 1 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 0 0 0 1 1 0 0 0 0 i 0 0 0 0 i 0 = 2 1 1 − 1 − 1 1 1 1 1 1 i − i i − i i i − i − i
U = 1 2 ( 1 1 i i − 1 1 − i i − 1 1 i − i 1 1 − i − i ) U = \frac{1}{2} \begin{pmatrix} 1 & 1 & i & i \\ -1 & 1 & -i & i \\ -1 & 1 & i & -i \\ 1 & 1 & -i & -i \end{pmatrix} U = 2 1 1 − 1 − 1 1 1 1 1 1 i − i i − i i i − i − i
결과: 회로의 유니터리 행렬은 1 2 ( 1 1 i i − 1 1 − i i − 1 1 i − i 1 1 − i − i ) \frac{1}{2} \begin{pmatrix} 1 & 1 & i & i \\ -1 & 1 & -i & i \\ -1 & 1 & i & -i \\ 1 & 1 & -i & -i \end{pmatrix} 2 1 1 − 1 − 1 1 1 1 1 1 i − i i − i i i − i − i
이 행렬은 ∣ q 1 q 0 ⟩ |q_1 q_0\rangle ∣ q 1 q 0 ⟩ ∣ 00 ⟩ , ∣ 01 ⟩ , ∣ 10 ⟩ , ∣ 11 ⟩ |00\rangle, |01\rangle, |10\rangle, |11\rangle ∣00 ⟩ , ∣01 ⟩ , ∣10 ⟩ , ∣11 ⟩
정규 직교 기저 { ∣ ψ 0 ⟩ , ∣ ψ 1 ⟩ } \{|\psi_0\rangle, |\psi_1\rangle\} { ∣ ψ 0 ⟩ , ∣ ψ 1 ⟩}
∣ ψ 0 ⟩ = 1 3 ∣ 0 ⟩ + 2 3 ∣ 1 ⟩ , ∣ ψ 1 ⟩ = 2 3 ∣ 0 ⟩ − 1 3 ∣ 1 ⟩ |\psi_0\rangle = \frac{1}{\sqrt{3}}|0\rangle + \sqrt{\frac{2}{3}}|1\rangle, \quad |\psi_1\rangle = \sqrt{\frac{2}{3}}|0\rangle - \frac{1}{\sqrt{3}}|1\rangle ∣ ψ 0 ⟩ = 3 1 ∣0 ⟩ + 3 2 ∣1 ⟩ , ∣ ψ 1 ⟩ = 3 2 ∣0 ⟩ − 3 1 ∣1 ⟩
사영 연산자를 다음과 같이 정의한다:
Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ , Π 1 = ∣ ψ 1 ⟩ ⟨ ψ 1 ∣ \Pi_0 = |\psi_0\rangle\langle\psi_0|, \quad \Pi_1 = |\psi_1\rangle\langle\psi_1| Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ , Π 1 = ∣ ψ 1 ⟩ ⟨ ψ 1 ∣
두 qubit이 다음 양자 상태에 있다:
∣ ψ ⟩ = 2 3 ∣ 00 ⟩ − 1 3 ∣ 01 ⟩ + 2 3 ∣ 10 ⟩ + 2 3 ∣ 11 ⟩ |\psi\rangle = \frac{\sqrt{2}}{3}|00\rangle - \frac{1}{3}|01\rangle + \frac{\sqrt{2}}{3}|10\rangle + \frac{2}{3}|11\rangle ∣ ψ ⟩ = 3 2 ∣00 ⟩ − 3 1 ∣01 ⟩ + 3 2 ∣10 ⟩ + 3 2 ∣11 ⟩
오른쪽 qubit을 사영 측정 { Π 0 , Π 1 } \{\Pi_0, \Pi_1\} { Π 0 , Π 1 } Π 0 \Pi_0 Π 0
사영 측정은 측정 연산자 { Π i } \{\Pi_i\} { Π i } 각 Π i \Pi_i Π i Π i 2 = Π i \Pi_i^2 = \Pi_i Π i 2 = Π i Π i † = Π i \Pi_i^\dagger = \Pi_i Π i † = Π i 완전성 조건: ∑ i Π i = I \sum_i \Pi_i = \mathbb{I} ∑ i Π i = I 결과 i i i Pr ( i ) = ⟨ ψ ∣ Π i ∣ ψ ⟩ = ∥ Π i ∣ ψ ⟩ ∥ 2 \text{Pr}(i) = \langle\psi|\Pi_i|\psi\rangle = \|\Pi_i|\psi\rangle\|^2 Pr ( i ) = ⟨ ψ ∣ Π i ∣ ψ ⟩ = ∥ Π i ∣ ψ ⟩ ∥ 2 다중 qubit 시스템에서 일부 qubit만 측정하는 것을 부분 측정이라고 합니다 두 qubit 시스템에서 오른쪽 qubit만 측정하는 경우, 측정 연산자는 I ⊗ Π \mathbb{I} \otimes \Pi I ⊗ Π 여기서 I \mathbb{I} I 두 qubit 상태 ∣ ψ ⟩ = ∑ a , b α a b ∣ a b ⟩ |\psi\rangle = \sum_{a,b} \alpha_{ab}|ab\rangle ∣ ψ ⟩ = ∑ a , b α ab ∣ ab ⟩ ∣ ϕ ⟩ = ∑ a , b β a b ∣ a b ⟩ |\phi\rangle = \sum_{a,b} \beta_{ab}|ab\rangle ∣ ϕ ⟩ = ∑ a , b β ab ∣ ab ⟩ ⟨ ψ ∣ ϕ ⟩ = ∑ a , b α ˉ a b β a b \langle\psi|\phi\rangle = \sum_{a,b} \bar{\alpha}_{ab}\beta_{ab} ⟨ ψ ∣ ϕ ⟩ = a , b ∑ α ˉ ab β ab
∣ ψ 0 ⟩ = 1 3 ∣ 0 ⟩ + 2 3 ∣ 1 ⟩ |\psi_0\rangle = \frac{1}{\sqrt{3}}|0\rangle + \sqrt{\frac{2}{3}}|1\rangle ∣ ψ 0 ⟩ = 3 1 ∣0 ⟩ + 3 2 ∣1 ⟩
Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ = ( 1 3 2 3 ) ( 1 3 2 3 ) = ( 1 3 2 3 2 3 2 3 ) \begin{aligned} \Pi_0 &= |\psi_0\rangle\langle\psi_0| \\ &= \begin{pmatrix} \frac{1}{\sqrt{3}} \\ \sqrt{\frac{2}{3}} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{3}} & \sqrt{\frac{2}{3}} \end{pmatrix} \\ &= \begin{pmatrix} \frac{1}{3} & \frac{\sqrt{2}}{3} \\ \frac{\sqrt{2}}{3} & \frac{2}{3} \end{pmatrix} \end{aligned} Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ = ( 3 1 3 2 ) ( 3 1 3 2 ) = ( 3 1 3 2 3 2 3 2 )
오른쪽 qubit만 측정하므로, 측정 연산자는 I ⊗ Π 0 \mathbb{I} \otimes \Pi_0 I ⊗ Π 0
I ⊗ Π 0 = ( 1 0 0 1 ) ⊗ ( 1 3 2 3 2 3 2 3 ) = ( 1 3 2 3 0 0 2 3 2 3 0 0 0 0 1 3 2 3 0 0 2 3 2 3 ) \mathbb{I} \otimes \Pi_0 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} \frac{1}{3} & \frac{\sqrt{2}}{3} \\ \frac{\sqrt{2}}{3} & \frac{2}{3} \end{pmatrix} = \begin{pmatrix} \frac{1}{3} & \frac{\sqrt{2}}{3} & 0 & 0 \\ \frac{\sqrt{2}}{3} & \frac{2}{3} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & \frac{\sqrt{2}}{3} \\ 0 & 0 & \frac{\sqrt{2}}{3} & \frac{2}{3} \end{pmatrix} I ⊗ Π 0 = ( 1 0 0 1 ) ⊗ ( 3 1 3 2 3 2 3 2 ) = 3 1 3 2 0 0 3 2 3 2 0 0 0 0 3 1 3 2 0 0 3 2 3 2
∣ ψ ⟩ = 2 3 ∣ 00 ⟩ − 1 3 ∣ 01 ⟩ + 2 3 ∣ 10 ⟩ + 2 3 ∣ 11 ⟩ |\psi\rangle = \frac{\sqrt{2}}{3}|00\rangle - \frac{1}{3}|01\rangle + \frac{\sqrt{2}}{3}|10\rangle + \frac{2}{3}|11\rangle ∣ ψ ⟩ = 3 2 ∣00 ⟩ − 3 1 ∣01 ⟩ + 3 2 ∣10 ⟩ + 3 2 ∣11 ⟩
∣ ψ ⟩ = ( 2 3 − 1 3 2 3 2 3 ) |\psi\rangle = \begin{pmatrix} \frac{\sqrt{2}}{3} \\ -\frac{1}{3} \\ \frac{\sqrt{2}}{3} \\ \frac{2}{3} \end{pmatrix} ∣ ψ ⟩ = 3 2 − 3 1 3 2 3 2
( I ⊗ Π 0 ) ∣ ψ ⟩ (\mathbb{I} \otimes \Pi_0)|\psi\rangle ( I ⊗ Π 0 ) ∣ ψ ⟩
( I ⊗ Π 0 ) ∣ ψ ⟩ = ( 1 3 2 3 0 0 2 3 2 3 0 0 0 0 1 3 2 3 0 0 2 3 2 3 ) ( 2 3 − 1 3 2 3 2 3 ) = ( 1 3 ⋅ 2 3 + 2 3 ⋅ ( − 1 3 ) 2 3 ⋅ 2 3 + 2 3 ⋅ ( − 1 3 ) 1 3 ⋅ 2 3 + 2 3 ⋅ 2 3 2 3 ⋅ 2 3 + 2 3 ⋅ 2 3 ) = ( 2 9 − 2 9 2 9 − 2 9 2 9 + 2 2 9 2 9 + 4 9 ) = ( 0 0 3 2 9 6 9 ) = ( 0 0 2 3 2 3 ) \begin{aligned} (\mathbb{I} \otimes \Pi_0)|\psi\rangle &= \begin{pmatrix} \frac{1}{3} & \frac{\sqrt{2}}{3} & 0 & 0 \\ \frac{\sqrt{2}}{3} & \frac{2}{3} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & \frac{\sqrt{2}}{3} \\ 0 & 0 & \frac{\sqrt{2}}{3} & \frac{2}{3} \end{pmatrix} \begin{pmatrix} \frac{\sqrt{2}}{3} \\ -\frac{1}{3} \\ \frac{\sqrt{2}}{3} \\ \frac{2}{3} \end{pmatrix} \\ &= \begin{pmatrix} \frac{1}{3} \cdot \frac{\sqrt{2}}{3} + \frac{\sqrt{2}}{3} \cdot \left(-\frac{1}{3}\right) \\ \frac{\sqrt{2}}{3} \cdot \frac{\sqrt{2}}{3} + \frac{2}{3} \cdot \left(-\frac{1}{3}\right) \\ \frac{1}{3} \cdot \frac{\sqrt{2}}{3} + \frac{\sqrt{2}}{3} \cdot \frac{2}{3} \\ \frac{\sqrt{2}}{3} \cdot \frac{\sqrt{2}}{3} + \frac{2}{3} \cdot \frac{2}{3} \end{pmatrix} \\ &= \begin{pmatrix} \frac{\sqrt{2}}{9} - \frac{\sqrt{2}}{9} \\ \frac{2}{9} - \frac{2}{9} \\ \frac{\sqrt{2}}{9} + \frac{2\sqrt{2}}{9} \\ \frac{2}{9} + \frac{4}{9} \end{pmatrix} \\ &= \begin{pmatrix} 0 \\ 0 \\ \frac{3\sqrt{2}}{9} \\ \frac{6}{9} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \frac{\sqrt{2}}{3} \\ \frac{2}{3} \end{pmatrix} \end{aligned} ( I ⊗ Π 0 ) ∣ ψ ⟩ = 3 1 3 2 0 0 3 2 3 2 0 0 0 0 3 1 3 2 0 0 3 2 3 2 3 2 − 3 1 3 2 3 2 = 3 1 ⋅ 3 2 + 3 2 ⋅ ( − 3 1 ) 3 2 ⋅ 3 2 + 3 2 ⋅ ( − 3 1 ) 3 1 ⋅ 3 2 + 3 2 ⋅ 3 2 3 2 ⋅ 3 2 + 3 2 ⋅ 3 2 = 9 2 − 9 2 9 2 − 9 2 9 2 + 9 2 2 9 2 + 9 4 = 0 0 9 3 2 9 6 = 0 0 3 2 3 2
결과 0을 얻을 확률은 ∥ ( I ⊗ Π 0 ) ∣ ψ ⟩ ∥ 2 \|(\mathbb{I} \otimes \Pi_0)|\psi\rangle\|^2 ∥ ( I ⊗ Π 0 ) ∣ ψ ⟩ ∥ 2
Pr ( 0 ) = ∥ ( 0 0 2 3 2 3 ) ∥ 2 = 0 2 + 0 2 + ( 2 3 ) 2 + ( 2 3 ) 2 = 2 9 + 4 9 = 6 9 = 2 3 \begin{aligned} \text{Pr}(0) &= \left\| \begin{pmatrix} 0 \\ 0 \\ \frac{\sqrt{2}}{3} \\ \frac{2}{3} \end{pmatrix} \right\|^2 \\ &= 0^2 + 0^2 + \left(\frac{\sqrt{2}}{3}\right)^2 + \left(\frac{2}{3}\right)^2 \\ &= \frac{2}{9} + \frac{4}{9} \\ &= \frac{6}{9} = \frac{2}{3} \end{aligned} Pr ( 0 ) = 0 0 3 2 3 2 2 = 0 2 + 0 2 + ( 3 2 ) 2 + ( 3 2 ) 2 = 9 2 + 9 4 = 9 6 = 3 2
결과: 결과 0을 얻을 확률은 2 3 \frac{2}{3} 3 2
사영 측정에서 부분 측정의 확률은 측정 연산자를 적용한 후의 상태 벡터의 노름 제곱으로 계산됩니다. 이 경우 오른쪽 qubit에 Π 0 \Pi_0 Π 0 ∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩ 2 3 \frac{2}{3} 3 2
다음 두 양자 상태를 완벽하게 구별할 수 있는가?
∣ ψ 0 ⟩ = 5 13 ∣ 0 ⟩ + 12 13 ∣ 1 ⟩ , ∣ ψ 1 ⟩ = 12 13 ∣ 0 ⟩ − 5 13 ∣ 1 ⟩ |\psi_0\rangle = \frac{5}{13}|0\rangle + \frac{12}{13}|1\rangle, \quad |\psi_1\rangle = \frac{12}{13}|0\rangle - \frac{5}{13}|1\rangle ∣ ψ 0 ⟩ = 13 5 ∣0 ⟩ + 13 12 ∣1 ⟩ , ∣ ψ 1 ⟩ = 13 12 ∣0 ⟩ − 13 5 ∣1 ⟩
두 양자 상태 ∣ ψ ⟩ |\psi\rangle ∣ ψ ⟩ ∣ ϕ ⟩ |\phi\rangle ∣ ϕ ⟩ ⟨ ψ ∣ ϕ ⟩ = 0 \langle\psi|\phi\rangle = 0 ⟨ ψ ∣ ϕ ⟩ = 0 직교하는 양자 상태는 완벽하게 구별 가능합니다 내적 계산: ⟨ ψ ∣ ϕ ⟩ = ∑ a α a ‾ β a \langle\psi|\phi\rangle = \sum_a \overline{\alpha_a}\beta_a ⟨ ψ ∣ ϕ ⟩ = ∑ a α a β a α a \alpha_a α a β a \beta_a β a 두 양자 상태를 완벽하게 구별한다는 것은 측정을 통해 항상 정확하게 어떤 상태인지 알 수 있다는 의미입니다 핵심 정리 : 두 양자 상태가 완벽하게 구별 가능한 필요충분조건은 두 상태가 직교하는 것입니다비직교 상태는 완벽하게 구별할 수 없습니다 (양자 정보의 제한사항) 직교하는 두 상태 ∣ ϕ ⟩ |\phi\rangle ∣ ϕ ⟩ ∣ ψ ⟩ |\psi\rangle ∣ ψ ⟩ ⟨ ϕ ∣ ψ ⟩ = 0 \langle\phi|\psi\rangle = 0 ⟨ ϕ ∣ ψ ⟩ = 0 측정 연산자: { Π 0 = ∣ ϕ ⟩ ⟨ ϕ ∣ , Π 1 = I − ∣ ϕ ⟩ ⟨ ϕ ∣ } \{\Pi_0 = |\phi\rangle\langle\phi|, \Pi_1 = \mathbb{I} - |\phi\rangle\langle\phi|\} { Π 0 = ∣ ϕ ⟩ ⟨ ϕ ∣ , Π 1 = I − ∣ ϕ ⟩ ⟨ ϕ ∣ } ∣ ϕ ⟩ |\phi\rangle ∣ ϕ ⟩ ∣ ψ ⟩ |\psi\rangle ∣ ψ ⟩ 비직교 상태 구별 불가 : 비직교 상태는 완벽하게 구별할 수 없습니다복제 불가 정리 : 알려지지 않은 양자 상태를 완벽하게 복제할 수 없습니다전역 위상의 무관성 : 전역 위상만 다른 두 상태는 물리적으로 동일합니다먼저 두 상태가 정규화되어 있는지 확인합니다:
∣ ψ 0 ⟩ |\psi_0\rangle ∣ ψ 0 ⟩
∥ ∣ ψ 0 ⟩ ∥ 2 = ∣ 5 13 ∣ 2 + ∣ 12 13 ∣ 2 = 25 169 + 144 169 = 169 169 = 1 \||\psi_0\rangle\|^2 = \left|\frac{5}{13}\right|^2 + \left|\frac{12}{13}\right|^2 = \frac{25}{169} + \frac{144}{169} = \frac{169}{169} = 1 ∥∣ ψ 0 ⟩ ∥ 2 = 13 5 2 + 13 12 2 = 169 25 + 169 144 = 169 169 = 1
∣ ψ 1 ⟩ |\psi_1\rangle ∣ ψ 1 ⟩
∥ ∣ ψ 1 ⟩ ∥ 2 = ∣ 12 13 ∣ 2 + ∣ − 5 13 ∣ 2 = 144 169 + 25 169 = 169 169 = 1 \||\psi_1\rangle\|^2 = \left|\frac{12}{13}\right|^2 + \left|-\frac{5}{13}\right|^2 = \frac{144}{169} + \frac{25}{169} = \frac{169}{169} = 1 ∥∣ ψ 1 ⟩ ∥ 2 = 13 12 2 + − 13 5 2 = 169 144 + 169 25 = 169 169 = 1
두 상태 모두 정규화되어 있습니다.
두 상태의 내적을 계산하여 직교 여부를 확인합니다:
⟨ ψ 0 ∣ ψ 1 ⟩ = ( 5 13 ⟨ 0 ∣ + 12 13 ⟨ 1 ∣ ) ( 12 13 ∣ 0 ⟩ − 5 13 ∣ 1 ⟩ ) = 5 13 ⋅ 12 13 ⟨ 0 ∣ 0 ⟩ − 5 13 ⋅ 5 13 ⟨ 0 ∣ 1 ⟩ + 12 13 ⋅ 12 13 ⟨ 1 ∣ 0 ⟩ − 12 13 ⋅ 5 13 ⟨ 1 ∣ 1 ⟩ = 60 169 − 0 + 0 − 60 169 = 0 \begin{aligned} \langle\psi_0|\psi_1\rangle &= \left(\frac{5}{13}\langle0| + \frac{12}{13}\langle1|\right)\left(\frac{12}{13}|0\rangle - \frac{5}{13}|1\rangle\right) \\ &= \frac{5}{13} \cdot \frac{12}{13}\langle0|0\rangle - \frac{5}{13} \cdot \frac{5}{13}\langle0|1\rangle + \frac{12}{13} \cdot \frac{12}{13}\langle1|0\rangle - \frac{12}{13} \cdot \frac{5}{13}\langle1|1\rangle \\ &= \frac{60}{169} - 0 + 0 - \frac{60}{169} \\ &= 0 \end{aligned} ⟨ ψ 0 ∣ ψ 1 ⟩ = ( 13 5 ⟨ 0∣ + 13 12 ⟨ 1∣ ) ( 13 12 ∣0 ⟩ − 13 5 ∣1 ⟩ ) = 13 5 ⋅ 13 12 ⟨ 0∣0 ⟩ − 13 5 ⋅ 13 5 ⟨ 0∣1 ⟩ + 13 12 ⋅ 13 12 ⟨ 1∣0 ⟩ − 13 12 ⋅ 13 5 ⟨ 1∣1 ⟩ = 169 60 − 0 + 0 − 169 60 = 0
여기서:
⟨ 0 ∣ 0 ⟩ = 1 \langle0|0\rangle = 1 ⟨ 0∣0 ⟩ = 1 ⟨ 1 ∣ 1 ⟩ = 1 \langle1|1\rangle = 1 ⟨ 1∣1 ⟩ = 1 ⟨ 0 ∣ 1 ⟩ = 0 \langle0|1\rangle = 0 ⟨ 0∣1 ⟩ = 0 ⟨ 1 ∣ 0 ⟩ = 0 \langle1|0\rangle = 0 ⟨ 1∣0 ⟩ = 0 ⟨ ψ 0 ∣ ψ 1 ⟩ = 0 \langle\psi_0|\psi_1\rangle = 0 ⟨ ψ 0 ∣ ψ 1 ⟩ = 0 직교 합니다.
양자 정보 이론의 핵심 정리에 따르면:
직교하는 양자 상태는 완벽하게 구별 가능합니다 사영 측정 { Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ , Π 1 = ∣ ψ 1 ⟩ ⟨ ψ 1 ∣ } \{\Pi_0 = |\psi_0\rangle\langle\psi_0|, \Pi_1 = |\psi_1\rangle\langle\psi_1|\} { Π 0 = ∣ ψ 0 ⟩ ⟨ ψ 0 ∣ , Π 1 = ∣ ψ 1 ⟩ ⟨ ψ 1 ∣ } ∣ ψ 0 ⟩ |\psi_0\rangle ∣ ψ 0 ⟩ ∣ ψ 1 ⟩ |\psi_1\rangle ∣ ψ 1 ⟩ 결과: 두 상태는 완벽하게 구별 가능합니다. 왜냐하면 두 상태가 직교하기 때문입니다.
두 상태의 내적이 0이므로 직교하며, 직교하는 양자 상태는 사영 측정을 통해 완벽하게 구별할 수 있습니다. 이는 양자 정보 이론의 기본 원리입니다.
목적 : 공유된 얽힘과 고전 통신을 사용하여 qubit을 전송하는 프로토콜요구사항 : 1 e-bit의 공유 얽힘 (Alice와 Bob이 Bell 상태 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 2 비트의 고전 통신 (Alice가 측정 결과 a a a b b b 결과 : qubit의 양자 정보가 완벽하게 전송됨알려지지 않은 상태 전송 : 전송되는 qubit Q의 상태는 Alice와 Bob 모두에게 알려지지 않았습니다상관관계 보존 : Q가 다른 시스템과 얽혀 있다면, 그 상관관계도 전송에 의해 보존됩니다복제 불가 : No-cloning theorem에 의해, 전송 후 Alice는 더 이상 원래 상태를 가지지 않습니다물질 전송 아님 : 양자 정보를 전송하는 것이지, 물질 자체를 전송하는 것이 아닙니다Alice는 CNOT 연산을 수행 (Q가 제어, A가 대상) Alice는 Q에 대해 Hadamard 연산을 수행 Alice는 A와 Q를 측정하여 각각 이진 결과 a a a b b b Alice는 a a a b b b Bob은 조건부 연산을 수행: a = 1 a=1 a = 1 b = 1 b=1 b = 1 양자 순간이동은 전송되는 qubit이 다른 시스템과 얽혀 있어도 작동합니다 이는 프로토콜의 중요한 특징으로, 얽힘 상태의 상관관계를 보존할 수 있습니다 양자 순간이동 프로토콜은 전송되는 qubit이 다른 시스템과 얽혀 있어도 작동하며, 그 상관관계를 보존할 수 있습니다. 이는 프로토콜의 중요한 특징으로, 얽힘 상태의 양자 상관관계를 유지하면서 정보를 전송할 수 있게 해줍니다.
Alice와 Bob이 CHSH 게임을 플레이하지만, ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩
네 가지 Bell 상태는 모두 1 e-bit의 얽힘을 나타냅니다:
∣ ϕ + ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ |\phi^+\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle ∣ ϕ + ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩ ∣ ϕ − ⟩ = 1 2 ∣ 00 ⟩ − 1 2 ∣ 11 ⟩ |\phi^-\rangle = \frac{1}{\sqrt{2}}|00\rangle - \frac{1}{\sqrt{2}}|11\rangle ∣ ϕ − ⟩ = 2 1 ∣00 ⟩ − 2 1 ∣11 ⟩ ∣ ψ + ⟩ = 1 2 ∣ 01 ⟩ + 1 2 ∣ 10 ⟩ |\psi^+\rangle = \frac{1}{\sqrt{2}}|01\rangle + \frac{1}{\sqrt{2}}|10\rangle ∣ ψ + ⟩ = 2 1 ∣01 ⟩ + 2 1 ∣10 ⟩ ∣ ψ − ⟩ = 1 2 ∣ 01 ⟩ − 1 2 ∣ 10 ⟩ |\psi^-\rangle = \frac{1}{\sqrt{2}}|01\rangle - \frac{1}{\sqrt{2}}|10\rangle ∣ ψ − ⟩ = 2 1 ∣01 ⟩ − 2 1 ∣10 ⟩ ( I ⊗ I ) ∣ ϕ + ⟩ = ∣ ϕ + ⟩ (\mathbb{I} \otimes \mathbb{I}) |\phi^+ \rangle = |\phi^+\rangle ( I ⊗ I ) ∣ ϕ + ⟩ = ∣ ϕ + ⟩ ( I ⊗ Z ) ∣ ϕ + ⟩ = ∣ ϕ − ⟩ (\mathbb{I} \otimes Z) |\phi^+ \rangle = |\phi^-\rangle ( I ⊗ Z ) ∣ ϕ + ⟩ = ∣ ϕ − ⟩ ( I ⊗ X ) ∣ ϕ + ⟩ = ∣ ψ + ⟩ (\mathbb{I} \otimes X) |\phi^+ \rangle = |\psi^+\rangle ( I ⊗ X ) ∣ ϕ + ⟩ = ∣ ψ + ⟩ ( I ⊗ X Z ) ∣ ϕ + ⟩ = ∣ ψ − ⟩ (\mathbb{I} \otimes XZ) |\phi^+ \rangle = |\psi^-\rangle ( I ⊗ XZ ) ∣ ϕ + ⟩ = ∣ ψ − ⟩ 따라서 Bob이 X Z XZ XZ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩
CHSH 게임에서 최대 승리 확률을 얻으려면 1 e-bit의 얽힘(즉, Bell 상태)이 필요합니다 표준 전략은 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ Bell 상태들은 모두 동일한 얽힘 양(1 e-bit)을 가지므로, 적절한 변환을 통해 동일한 전략을 사용할 수 있습니다 모든 Bell 상태는 정확히 1 e-bit의 얽힘을 나타냅니다 ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 두 상태는 서로 다른 구조를 가지며, ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ 01 ⟩ |01\rangle ∣01 ⟩ ∣ 10 ⟩ |10\rangle ∣10 ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ 00 ⟩ |00\rangle ∣00 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩
( I ⊗ X Z ) ∣ ϕ + ⟩ = ∣ ψ − ⟩ (\mathbb{I} \otimes XZ) |\phi^+ \rangle = |\psi^-\rangle ( I ⊗ XZ ) ∣ ϕ + ⟩ = ∣ ψ − ⟩
따라서 Bob이 자신의 qubit에 X Z XZ XZ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩
역변환도 가능합니다:
( I ⊗ X Z ) ∣ ψ − ⟩ = ( I ⊗ X Z ) ( I ⊗ X Z ) ∣ ϕ + ⟩ = ( I ⊗ X Z X Z ) ∣ ϕ + ⟩ (\mathbb{I} \otimes XZ) |\psi^- \rangle = (\mathbb{I} \otimes XZ)(\mathbb{I} \otimes XZ) |\phi^+ \rangle = (\mathbb{I} \otimes XZXZ) |\phi^+ \rangle ( I ⊗ XZ ) ∣ ψ − ⟩ = ( I ⊗ XZ ) ( I ⊗ XZ ) ∣ ϕ + ⟩ = ( I ⊗ XZXZ ) ∣ ϕ + ⟩
X Z X Z = − X Z X Z = − I XZXZ = -XZXZ = -I XZXZ = − XZXZ = − I
X Z = ( 0 1 1 0 ) ( 1 0 0 − 1 ) = ( 0 − 1 1 0 ) XZ = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} XZ = ( 0 1 1 0 ) ( 1 0 0 − 1 ) = ( 0 1 − 1 0 )
( X Z ) 2 = − I (XZ)^2 = -I ( XZ ) 2 = − I ( I ⊗ X Z ) 2 ∣ ϕ + ⟩ = − ∣ ϕ + ⟩ (\mathbb{I} \otimes XZ)^2 |\phi^+\rangle = -|\phi^+\rangle ( I ⊗ XZ ) 2 ∣ ϕ + ⟩ = − ∣ ϕ + ⟩
하지만 더 간단하게, Bob이 게임 시작 전에 자신의 qubit에 X Z XZ XZ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩
∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ 두 상태 모두 동일한 얽힘 양을 가지므로, CHSH 게임에서 동일한 성능을 발휘할 수 있습니다.
CHSH 게임의 표준 양자 전략은 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩
만약 Alice와 Bob이 ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩
Bob이 게임 시작 전에 자신의 qubit에 적절한 유니터리 연산(예: X Z XZ XZ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 이 변환은 통신 없이 Bob이 독립적으로 수행할 수 있습니다 변환 후 표준 CHSH 전략을 사용하여 Tsirelson 부등식이 허용하는 최대 확률로 이길 수 있습니다 Alice와 Bob은 여전히 최대 확률로 이길 수 있습니다. 왜냐하면 Alice와 Bob이 통신 없이 ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩
∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩
다음 행렬 M M M
M = ( 2 − 1 − 9 3 ) M = \begin{pmatrix} 2 & -1 \\ -9 & 3 \end{pmatrix} M = ( 2 − 9 − 1 3 )
표준 기저 벡터:
∣ 0 ⟩ = ( 1 0 ) |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} ∣0 ⟩ = ( 1 0 ) ∣ 1 ⟩ = ( 0 1 ) |1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} ∣1 ⟩ = ( 0 1 ) ∣ i ⟩ ⟨ j ∣ |i\rangle\langle j| ∣ i ⟩ ⟨ j ∣ ∣ i ⟩ |i\rangle ∣ i ⟩ ⟨ j ∣ \langle j| ⟨ j ∣ 결과는 행렬이 되며, ( i , j ) (i,j) ( i , j ) 예: ∣ 0 ⟩ ⟨ 0 ∣ = ( 1 0 ) ( 1 0 ) = ( 1 0 0 0 ) |0\rangle\langle0| = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} ∣0 ⟩ ⟨ 0∣ = ( 1 0 ) ( 1 0 ) = ( 1 0 0 0 ) 행렬 M M M ( i , j ) (i,j) ( i , j ) M i j = ⟨ i ∣ M ∣ j ⟩ M_{ij} = \langle i|M|j\rangle M ij = ⟨ i ∣ M ∣ j ⟩ 표준 기저에서 ∣ i ⟩ |i\rangle ∣ i ⟩ ∣ j ⟩ |j\rangle ∣ j ⟩ M i j M_{ij} M ij 주어진 행렬:
M = ( 2 − 1 − 9 3 ) M = \begin{pmatrix} 2 & -1 \\ -9 & 3 \end{pmatrix} M = ( 2 − 9 − 1 3 )
행렬 성분:
M 00 = 2 M_{00} = 2 M 00 = 2 M 01 = − 1 M_{01} = -1 M 01 = − 1 M 10 = − 9 M_{10} = -9 M 10 = − 9 M 11 = 3 M_{11} = 3 M 11 = 3 행렬을 Dirac notation으로 표현:
M = M 00 ∣ 0 ⟩ ⟨ 0 ∣ + M 01 ∣ 0 ⟩ ⟨ 1 ∣ + M 10 ∣ 1 ⟩ ⟨ 0 ∣ + M 11 ∣ 1 ⟩ ⟨ 1 ∣ = 2 ∣ 0 ⟩ ⟨ 0 ∣ + ( − 1 ) ∣ 0 ⟩ ⟨ 1 ∣ + ( − 9 ) ∣ 1 ⟩ ⟨ 0 ∣ + 3 ∣ 1 ⟩ ⟨ 1 ∣ = 2 ∣ 0 ⟩ ⟨ 0 ∣ − ∣ 0 ⟩ ⟨ 1 ∣ − 9 ∣ 1 ⟩ ⟨ 0 ∣ + 3 ∣ 1 ⟩ ⟨ 1 ∣ \begin{aligned} M &= M_{00}|0\rangle\langle0| + M_{01}|0\rangle\langle1| + M_{10}|1\rangle\langle0| + M_{11}|1\rangle\langle1| \\ &= 2|0\rangle\langle0| + (-1)|0\rangle\langle1| + (-9)|1\rangle\langle0| + 3|1\rangle\langle1| \\ &= 2|0\rangle\langle0| - |0\rangle\langle1| - 9|1\rangle\langle0| + 3|1\rangle\langle1| \end{aligned} M = M 00 ∣0 ⟩ ⟨ 0∣ + M 01 ∣0 ⟩ ⟨ 1∣ + M 10 ∣1 ⟩ ⟨ 0∣ + M 11 ∣1 ⟩ ⟨ 1∣ = 2∣0 ⟩ ⟨ 0∣ + ( − 1 ) ∣0 ⟩ ⟨ 1∣ + ( − 9 ) ∣1 ⟩ ⟨ 0∣ + 3∣1 ⟩ ⟨ 1∣ = 2∣0 ⟩ ⟨ 0∣ − ∣0 ⟩ ⟨ 1∣ − 9∣1 ⟩ ⟨ 0∣ + 3∣1 ⟩ ⟨ 1∣
각 항이 올바른 행렬을 만드는지 확인:
2 ∣ 0 ⟩ ⟨ 0 ∣ = 2 ( 1 0 ) ( 1 0 ) = 2 ( 1 0 0 0 ) = ( 2 0 0 0 ) 2|0\rangle\langle0| = 2\begin{pmatrix} 1 \\ 0 \end{pmatrix}\begin{pmatrix} 1 & 0 \end{pmatrix} = 2\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & 0 \end{pmatrix} 2∣0 ⟩ ⟨ 0∣ = 2 ( 1 0 ) ( 1 0 ) = 2 ( 1 0 0 0 ) = ( 2 0 0 0 ) − ∣ 0 ⟩ ⟨ 1 ∣ = − ( 1 0 ) ( 0 1 ) = − ( 0 1 0 0 ) = ( 0 − 1 0 0 ) -|0\rangle\langle1| = -\begin{pmatrix} 1 \\ 0 \end{pmatrix}\begin{pmatrix} 0 & 1 \end{pmatrix} = -\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 0 & 0 \end{pmatrix} − ∣0 ⟩ ⟨ 1∣ = − ( 1 0 ) ( 0 1 ) = − ( 0 0 1 0 ) = ( 0 0 − 1 0 ) − 9 ∣ 1 ⟩ ⟨ 0 ∣ = − 9 ( 0 1 ) ( 1 0 ) = − 9 ( 0 0 1 0 ) = ( 0 0 − 9 0 ) -9|1\rangle\langle0| = -9\begin{pmatrix} 0 \\ 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \end{pmatrix} = -9\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ -9 & 0 \end{pmatrix} − 9∣1 ⟩ ⟨ 0∣ = − 9 ( 0 1 ) ( 1 0 ) = − 9 ( 0 1 0 0 ) = ( 0 − 9 0 0 ) 3 ∣ 1 ⟩ ⟨ 1 ∣ = 3 ( 0 1 ) ( 0 1 ) = 3 ( 0 0 0 1 ) = ( 0 0 0 3 ) 3|1\rangle\langle1| = 3\begin{pmatrix} 0 \\ 1 \end{pmatrix}\begin{pmatrix} 0 & 1 \end{pmatrix} = 3\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 3 \end{pmatrix} 3∣1 ⟩ ⟨ 1∣ = 3 ( 0 1 ) ( 0 1 ) = 3 ( 0 0 0 1 ) = ( 0 0 0 3 ) 합산:
( 2 0 0 0 ) + ( 0 − 1 0 0 ) + ( 0 0 − 9 0 ) + ( 0 0 0 3 ) = ( 2 − 1 − 9 3 ) \begin{pmatrix} 2 & 0 \\ 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & -1 \\ 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 \\ -9 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 \\ 0 & 3 \end{pmatrix} = \begin{pmatrix} 2 & -1 \\ -9 & 3 \end{pmatrix} ( 2 0 0 0 ) + ( 0 0 − 1 0 ) + ( 0 − 9 0 0 ) + ( 0 0 0 3 ) = ( 2 − 9 − 1 3 )
검증 완료.
M = 2 ∣ 0 ⟩ ⟨ 0 ∣ − ∣ 0 ⟩ ⟨ 1 ∣ − 9 ∣ 1 ⟩ ⟨ 0 ∣ + 3 ∣ 1 ⟩ ⟨ 1 ∣ M = 2|0\rangle\langle0| - |0\rangle\langle1| - 9|1\rangle\langle0| + 3|1\rangle\langle1| M = 2∣0 ⟩ ⟨ 0∣ − ∣0 ⟩ ⟨ 1∣ − 9∣1 ⟩ ⟨ 0∣ + 3∣1 ⟩ ⟨ 1∣
행렬의 각 성분을 해당하는 외적 ∣ i ⟩ ⟨ j ∣ |i\rangle\langle j| ∣ i ⟩ ⟨ j ∣
Γ = { ♣ , ♢ , ♡ , ♠ } \Gamma = \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} Γ = { ♣ , ♢ , ♡ , ♠ } ♣ \clubsuit ♣ Γ × Γ \Gamma \times \Gamma Γ × Γ
두 집합 Σ \Sigma Σ Γ \Gamma Γ Σ × Γ = { ( a , b ) : a ∈ Σ 그리고 b ∈ Γ } \Sigma \times \Gamma = \{(a, b): a \in \Sigma \text{ 그리고 } b \in \Gamma\} Σ × Γ = {( a , b ) : a ∈ Σ 그리고 b ∈ Γ }
Γ × Γ \Gamma \times \Gamma Γ × Γ Γ \Gamma Γ ∣ Γ ∣ = n |\Gamma| = n ∣Γ∣ = n ∣ Γ × Γ ∣ = n 2 |\Gamma \times \Gamma| = n^2 ∣Γ × Γ∣ = n 2 카르테시안 곱의 원소들은 사전식 순서로 정렬됩니다 규칙 : 왼쪽에서 오른쪽으로 갈수록 중요도가 감소합니다첫 번째 원소가 같으면 두 번째 원소로 비교합니다 사전에서 단어를 정렬하는 방식과 동일합니다 { 0 , 1 } × { 0 , 1 } \{0,1\} \times \{0,1\} { 0 , 1 } × { 0 , 1 } ( 0 , 0 ) , ( 0 , 1 ) , ( 1 , 0 ) , ( 1 , 1 ) (0,0), (0,1), (1,0), (1,1) ( 0 , 0 ) , ( 0 , 1 ) , ( 1 , 0 ) , ( 1 , 1 ) { 1 , 2 , 3 } × { 0 , 1 } \{1,2,3\} \times \{0,1\} { 1 , 2 , 3 } × { 0 , 1 } ( 1 , 0 ) , ( 1 , 1 ) , ( 2 , 0 ) , ( 2 , 1 ) , ( 3 , 0 ) , ( 3 , 1 ) (1,0), (1,1), (2,0), (2,1), (3,0), (3,1) ( 1 , 0 ) , ( 1 , 1 ) , ( 2 , 0 ) , ( 2 , 1 ) , ( 3 , 0 ) , ( 3 , 1 ) Γ = { ♣ , ♢ , ♡ , ♠ } \Gamma = \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\} Γ = { ♣ , ♢ , ♡ , ♠ } ∣ Γ ∣ = 4 |\Gamma| = 4 ∣Γ∣ = 4
따라서 ∣ Γ × Γ ∣ = 4 × 4 = 16 |\Gamma \times \Gamma| = 4 \times 4 = 16 ∣Γ × Γ∣ = 4 × 4 = 16
12번째 원소가 존재합니다 (선택지 D는 틀림).
Γ \Gamma Γ ♣ \clubsuit ♣ ♢ \diamondsuit ♢ ♡ \heartsuit ♡ ♠ \spadesuit ♠
사전식 순서로 Γ × Γ \Gamma \times \Gamma Γ × Γ
( ♣ , ♣ ) (\clubsuit, \clubsuit) ( ♣ , ♣ ) ( ♣ , ♢ ) (\clubsuit, \diamondsuit) ( ♣ , ♢ ) ( ♣ , ♡ ) (\clubsuit, \heartsuit) ( ♣ , ♡ ) ( ♣ , ♠ ) (\clubsuit, \spadesuit) ( ♣ , ♠ ) ( ♢ , ♣ ) (\diamondsuit, \clubsuit) ( ♢ , ♣ ) ( ♢ , ♢ ) (\diamondsuit, \diamondsuit) ( ♢ , ♢ ) ( ♢ , ♡ ) (\diamondsuit, \heartsuit) ( ♢ , ♡ ) ( ♢ , ♠ ) (\diamondsuit, \spadesuit) ( ♢ , ♠ ) ( ♡ , ♣ ) (\heartsuit, \clubsuit) ( ♡ , ♣ ) ( ♡ , ♢ ) (\heartsuit, \diamondsuit) ( ♡ , ♢ ) ( ♡ , ♡ ) (\heartsuit, \heartsuit) ( ♡ , ♡ ) ( ♡ , ♠ ) (\heartsuit, \spadesuit) ( ♡ , ♠ ) 12번째 원소 ( ♠ , ♣ ) (\spadesuit, \clubsuit) ( ♠ , ♣ ) ( ♠ , ♢ ) (\spadesuit, \diamondsuit) ( ♠ , ♢ ) ( ♠ , ♡ ) (\spadesuit, \heartsuit) ( ♠ , ♡ ) ( ♠ , ♠ ) (\spadesuit, \spadesuit) ( ♠ , ♠ ) 첫 번째 원소가 ♣ \clubsuit ♣ 첫 번째 원소가 ♢ \diamondsuit ♢ 첫 번째 원소가 ♡ \heartsuit ♡ 첫 번째 원소가 ♠ \spadesuit ♠ 12번째 원소는 첫 번째 원소가 ♡ \heartsuit ♡
12번째 원소는 ( ♡ , ♠ ) (\heartsuit, \spadesuit) ( ♡ , ♠ )
사전식 순서에서 왼쪽 원소가 더 중요하므로, 첫 번째 원소가 ♡ \heartsuit ♡ ♠ \spadesuit ♠
다음 네 벡터를 정의하자:
∣ u ⟩ = ( − 2 1 ) |u\rangle = \begin{pmatrix} -2 \\ 1 \end{pmatrix} ∣ u ⟩ = ( − 2 1 ) ∣ v ⟩ = ( 1 0 1 ) |v\rangle = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} ∣ v ⟩ = 1 0 1 ∣ w ⟩ = ( 4 1 ) |w\rangle = \begin{pmatrix} 4 \\ 1 \end{pmatrix} ∣ w ⟩ = ( 4 1 ) ∣ x ⟩ = ( 1 / 2 1 / 2 1 / 2 ) |x\rangle = \begin{pmatrix} 1/2 \\ 1/2 \\ 1/2 \end{pmatrix} ∣ x ⟩ = 1/2 1/2 1/2 다음 중 ∣ u ⟩ ⊗ ∣ v ⟩ − 2 3 ∣ w ⟩ ⊗ ∣ x ⟩ |u\rangle \otimes |v\rangle - \frac{2}{3}|w\rangle \otimes |x\rangle ∣ u ⟩ ⊗ ∣ v ⟩ − 3 2 ∣ w ⟩ ⊗ ∣ x ⟩
m × 1 m \times 1 m × 1 n × 1 n \times 1 n × 1 m n × 1 mn \times 1 mn × 1 예: 2 × 1 2 \times 1 2 × 1 3 × 1 3 \times 1 3 × 1 6 × 1 6 \times 1 6 × 1 텐서 곱에 스칼라를 곱하면 각 성분에 스칼라를 곱합니다 같은 차원의 벡터끼리 뺄셈은 각 성분별로 뺄셈합니다 차원 체크 : ∣ u ⟩ |u\rangle ∣ u ⟩ 2 × 1 2 \times 1 2 × 1 ∣ v ⟩ |v\rangle ∣ v ⟩ 3 × 1 3 \times 1 3 × 1 6 × 1 6 \times 1 6 × 1 2 × 3 = 6 2 \times 3 = 6 2 × 3 = 6
텐서 곱 계산 공식 :
( a b ) ⊗ ∣ v ⟩ = ( a ∣ v ⟩ b ∣ v ⟩ ) \begin{pmatrix} a \\ b \end{pmatrix} \otimes |v\rangle = \begin{pmatrix} a|v\rangle \\ b|v\rangle \end{pmatrix} ( a b ) ⊗ ∣ v ⟩ = ( a ∣ v ⟩ b ∣ v ⟩ )
∣ u ⟩ ⊗ ∣ v ⟩ = ( − 2 1 ) ⊗ ( 1 0 1 ) = ( − 2 ⋅ ( 1 0 1 ) 1 ⋅ ( 1 0 1 ) ) = ( − 2 ⋅ 1 − 2 ⋅ 0 − 2 ⋅ 1 1 ⋅ 1 1 ⋅ 0 1 ⋅ 1 ) = ( − 2 0 − 2 1 0 1 ) \begin{aligned} |u\rangle \otimes |v\rangle &= \begin{pmatrix} -2 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} -2 \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\ 1 \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \end{pmatrix} \\ &= \begin{pmatrix} -2 \cdot 1 \\ -2 \cdot 0 \\ -2 \cdot 1 \\ 1 \cdot 1 \\ 1 \cdot 0 \\ 1 \cdot 1 \end{pmatrix} \\ &= \begin{pmatrix} -2 \\ 0 \\ -2 \\ 1 \\ 0 \\ 1 \end{pmatrix} \end{aligned} ∣ u ⟩ ⊗ ∣ v ⟩ = ( − 2 1 ) ⊗ 1 0 1 = − 2 ⋅ 1 0 1 1 ⋅ 1 0 1 = − 2 ⋅ 1 − 2 ⋅ 0 − 2 ⋅ 1 1 ⋅ 1 1 ⋅ 0 1 ⋅ 1 = − 2 0 − 2 1 0 1
검증 : 결과 벡터의 길이가 6인지 확인합니다.
∣ w ⟩ |w\rangle ∣ w ⟩ 2 × 1 2 \times 1 2 × 1 ∣ x ⟩ |x\rangle ∣ x ⟩ 3 × 1 3 \times 1 3 × 1 6 × 1 6 \times 1 6 × 1
∣ w ⟩ ⊗ ∣ x ⟩ = ( 4 1 ) ⊗ ( 1 / 2 1 / 2 1 / 2 ) = ( 4 ⋅ ( 1 / 2 ) 4 ⋅ ( 1 / 2 ) 4 ⋅ ( 1 / 2 ) 1 ⋅ ( 1 / 2 ) 1 ⋅ ( 1 / 2 ) 1 ⋅ ( 1 / 2 ) ) = ( 2 2 2 1 / 2 1 / 2 1 / 2 ) \begin{aligned} |w\rangle \otimes |x\rangle &= \begin{pmatrix} 4 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1/2 \\ 1/2 \\ 1/2 \end{pmatrix} \\ &= \begin{pmatrix} 4 \cdot (1/2) \\ 4 \cdot (1/2) \\ 4 \cdot (1/2) \\ 1 \cdot (1/2) \\ 1 \cdot (1/2) \\ 1 \cdot (1/2) \end{pmatrix} \\ &= \begin{pmatrix} 2 \\ 2 \\ 2 \\ 1/2 \\ 1/2 \\ 1/2 \end{pmatrix} \end{aligned} ∣ w ⟩ ⊗ ∣ x ⟩ = ( 4 1 ) ⊗ 1/2 1/2 1/2 = 4 ⋅ ( 1/2 ) 4 ⋅ ( 1/2 ) 4 ⋅ ( 1/2 ) 1 ⋅ ( 1/2 ) 1 ⋅ ( 1/2 ) 1 ⋅ ( 1/2 ) = 2 2 2 1/2 1/2 1/2
2 3 ∣ w ⟩ ⊗ ∣ x ⟩ = 2 3 ( 2 2 2 1 / 2 1 / 2 1 / 2 ) = ( 4 / 3 4 / 3 4 / 3 1 / 3 1 / 3 1 / 3 ) \begin{aligned} \frac{2}{3}|w\rangle \otimes |x\rangle &= \frac{2}{3} \begin{pmatrix} 2 \\ 2 \\ 2 \\ 1/2 \\ 1/2 \\ 1/2 \end{pmatrix} \\ &= \begin{pmatrix} 4/3 \\ 4/3 \\ 4/3 \\ 1/3 \\ 1/3 \\ 1/3 \end{pmatrix} \end{aligned} 3 2 ∣ w ⟩ ⊗ ∣ x ⟩ = 3 2 2 2 2 1/2 1/2 1/2 = 4/3 4/3 4/3 1/3 1/3 1/3
∣ u ⟩ ⊗ ∣ v ⟩ − 2 3 ∣ w ⟩ ⊗ ∣ x ⟩ = ( − 2 0 − 2 1 0 1 ) − ( 4 / 3 4 / 3 4 / 3 1 / 3 1 / 3 1 / 3 ) = ( − 2 − 4 / 3 0 − 4 / 3 − 2 − 4 / 3 1 − 1 / 3 0 − 1 / 3 1 − 1 / 3 ) = ( − 10 / 3 − 4 / 3 − 10 / 3 2 / 3 − 1 / 3 2 / 3 ) = 1 3 ( − 10 − 4 − 10 2 − 1 2 ) \begin{aligned} |u\rangle \otimes |v\rangle - \frac{2}{3}|w\rangle \otimes |x\rangle &= \begin{pmatrix} -2 \\ 0 \\ -2 \\ 1 \\ 0 \\ 1 \end{pmatrix} - \begin{pmatrix} 4/3 \\ 4/3 \\ 4/3 \\ 1/3 \\ 1/3 \\ 1/3 \end{pmatrix} \\ &= \begin{pmatrix} -2 - 4/3 \\ 0 - 4/3 \\ -2 - 4/3 \\ 1 - 1/3 \\ 0 - 1/3 \\ 1 - 1/3 \end{pmatrix} \\ &= \begin{pmatrix} -10/3 \\ -4/3 \\ -10/3 \\ 2/3 \\ -1/3 \\ 2/3 \end{pmatrix} \\ &= \frac{1}{3} \begin{pmatrix} -10 \\ -4 \\ -10 \\ 2 \\ -1 \\ 2 \end{pmatrix} \end{aligned} ∣ u ⟩ ⊗ ∣ v ⟩ − 3 2 ∣ w ⟩ ⊗ ∣ x ⟩ = − 2 0 − 2 1 0 1 − 4/3 4/3 4/3 1/3 1/3 1/3 = − 2 − 4/3 0 − 4/3 − 2 − 4/3 1 − 1/3 0 − 1/3 1 − 1/3 = − 10/3 − 4/3 − 10/3 2/3 − 1/3 2/3 = 3 1 − 10 − 4 − 10 2 − 1 2
∣ u ⟩ ⊗ ∣ v ⟩ − 2 3 ∣ w ⟩ ⊗ ∣ x ⟩ = 1 3 ( − 10 − 4 − 10 2 − 1 2 ) |u\rangle \otimes |v\rangle - \frac{2}{3}|w\rangle \otimes |x\rangle = \frac{1}{3} \begin{pmatrix} -10 \\ -4 \\ -10 \\ 2 \\ -1 \\ 2 \end{pmatrix} ∣ u ⟩ ⊗ ∣ v ⟩ − 3 2 ∣ w ⟩ ⊗ ∣ x ⟩ = 3 1 − 10 − 4 − 10 2 − 1 2
텐서 곱은 각 벡터의 성분을 곱하여 새로운 벡터를 만듭니다. 2 × 1 2 \times 1 2 × 1 3 × 1 3 \times 1 3 × 1 6 × 1 6 \times 1 6 × 1
세 qubit 시스템이 다음 상태에 있다:
∣ ψ ⟩ = ∣ 0 ⟩ ∣ + ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ − ∣ 1 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ 3 |\psi\rangle = \frac{|0\rangle|+\rangle + |1\rangle|0\rangle|0\rangle - |1\rangle|1\rangle|1\rangle}{\sqrt{3}} ∣ ψ ⟩ = 3 ∣0 ⟩ ∣ + ⟩ + ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ − ∣1 ⟩ ∣1 ⟩ ∣1 ⟩
중간 qubit에 표준 기저 측정을 수행한다. 측정 결과가 0일 확률을 p 0 p_0 p 0 ∣ ψ 0 ⟩ |\psi_0\rangle ∣ ψ 0 ⟩ p 0 p_0 p 0 ∣ ψ 0 ⟩ |\psi_0\rangle ∣ ψ 0 ⟩
다중 qubit 시스템에서 일부 qubit만 측정하는 것을 부분 측정이라고 합니다 측정되지 않은 qubit의 상태는 측정 결과에 따라 조건부로 결정됩니다 측정 결과가 0일 때의 조건부 상태는 중간 qubit이 ∣ 0 ⟩ |0\rangle ∣0 ⟩ 측정 후 상태:∣ ψ 0 ⟩ = 1 p 0 ∑ a , c α a 0 c ∣ a ⟩ ∣ 0 ⟩ ∣ c ⟩ |\psi_0\rangle = \frac{1}{\sqrt{p_0}} \sum_{a,c} \alpha_{a0c}|a\rangle|0\rangle|c\rangle ∣ ψ 0 ⟩ = p 0 1 a , c ∑ α a 0 c ∣ a ⟩ ∣0 ⟩ ∣ c ⟩
∣ + ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) ∣ + ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) 표준 기저로 표현하면 두 항의 중첩입니다 주어진 상태를 세 qubit 모두 표준 기저로 표현합니다. 세 qubit을 ∣ q 0 q 1 q 2 ⟩ |q_0 q_1 q_2\rangle ∣ q 0 q 1 q 2 ⟩
중요 : ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ ∣ + ⟩ |+\rangle ∣ + ⟩
올바른 해석 : 세 qubit 시스템에서 ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ |1\rangle|0\rangle|0\rangle ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ |1\rangle|1\rangle|1\rangle ∣1 ⟩ ∣1 ⟩ ∣1 ⟩
따라서 ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ ? ⟩ |0\rangle|+\rangle|?\rangle ∣0 ⟩ ∣ + ⟩ ∣ ?⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ⊗ ∣ + ⟩ ⊗ ∣ 0 ⟩ |0\rangle \otimes |+\rangle \otimes |0\rangle ∣0 ⟩ ⊗ ∣ + ⟩ ⊗ ∣0 ⟩
표준 해석 : ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle|+\rangle|0\rangle ∣0 ⟩ ∣ + ⟩ ∣0 ⟩
∣ ψ ⟩ = ∣ 0 ⟩ ∣ + ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ − ∣ 1 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ 3 = 1 3 [ ∣ 0 ⟩ ⋅ 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⋅ ∣ 0 ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ − ∣ 1 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ ] = 1 3 [ 1 2 ∣ 0 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ + 1 2 ∣ 0 ⟩ ∣ 1 ⟩ ∣ 0 ⟩ + ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ − ∣ 1 ⟩ ∣ 1 ⟩ ∣ 1 ⟩ ] = 1 3 [ 1 2 ∣ 000 ⟩ + 1 2 ∣ 010 ⟩ + ∣ 100 ⟩ − ∣ 111 ⟩ ] \begin{aligned} |\psi\rangle &= \frac{|0\rangle|+\rangle + |1\rangle|0\rangle|0\rangle - |1\rangle|1\rangle|1\rangle}{\sqrt{3}} \\ &= \frac{1}{\sqrt{3}}\left[|0\rangle \cdot \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \cdot |0\rangle + |1\rangle|0\rangle|0\rangle - |1\rangle|1\rangle|1\rangle\right] \\ &= \frac{1}{\sqrt{3}}\left[\frac{1}{\sqrt{2}}|0\rangle|0\rangle|0\rangle + \frac{1}{\sqrt{2}}|0\rangle|1\rangle|0\rangle + |1\rangle|0\rangle|0\rangle - |1\rangle|1\rangle|1\rangle\right] \\ &= \frac{1}{\sqrt{3}}\left[\frac{1}{\sqrt{2}}|000\rangle + \frac{1}{\sqrt{2}}|010\rangle + |100\rangle - |111\rangle\right] \end{aligned} ∣ ψ ⟩ = 3 ∣0 ⟩ ∣ + ⟩ + ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ − ∣1 ⟩ ∣1 ⟩ ∣1 ⟩ = 3 1 [ ∣0 ⟩ ⋅ 2 1 ( ∣0 ⟩ + ∣1 ⟩) ⋅ ∣0 ⟩ + ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ − ∣1 ⟩ ∣1 ⟩ ∣1 ⟩ ] = 3 1 [ 2 1 ∣0 ⟩ ∣0 ⟩ ∣0 ⟩ + 2 1 ∣0 ⟩ ∣1 ⟩ ∣0 ⟩ + ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ − ∣1 ⟩ ∣1 ⟩ ∣1 ⟩ ] = 3 1 [ 2 1 ∣000 ⟩ + 2 1 ∣010 ⟩ + ∣100 ⟩ − ∣111 ⟩ ]
중간 qubit(두 번째 qubit, q 1 q_1 q 1 ∣ 0 ⟩ |0\rangle ∣0 ⟩
1 3 ⋅ 1 2 ∣ 000 ⟩ = 1 6 ∣ 000 ⟩ \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{2}}|000\rangle = \frac{1}{\sqrt{6}}|000\rangle 3 1 ⋅ 2 1 ∣000 ⟩ = 6 1 ∣000 ⟩ 1 3 ∣ 100 ⟩ = 1 3 ∣ 100 ⟩ \frac{1}{\sqrt{3}}|100\rangle = \frac{1}{\sqrt{3}}|100\rangle 3 1 ∣100 ⟩ = 3 1 ∣100 ⟩ 중간 qubit이 ∣ 0 ⟩ |0\rangle ∣0 ⟩
p 0 = ∣ 1 6 ∣ 2 + ∣ 1 3 ∣ 2 = 1 6 + 1 3 = 1 6 + 2 6 = 3 6 = 1 2 \begin{aligned} p_0 &= \left|\frac{1}{\sqrt{6}}\right|^2 + \left|\frac{1}{\sqrt{3}}\right|^2 \\ &= \frac{1}{6} + \frac{1}{3} \\ &= \frac{1}{6} + \frac{2}{6} \\ &= \frac{3}{6} = \frac{1}{2} \end{aligned} p 0 = 6 1 2 + 3 1 2 = 6 1 + 3 1 = 6 1 + 6 2 = 6 3 = 2 1
측정 결과가 0일 때의 조건부 상태는 중간 qubit이 ∣ 0 ⟩ |0\rangle ∣0 ⟩
∣ ψ 0 ⟩ = 1 p 0 ( 1 6 ∣ 000 ⟩ + 1 3 ∣ 100 ⟩ ) = 1 1 / 2 ( 1 6 ∣ 000 ⟩ + 1 3 ∣ 100 ⟩ ) = 2 ( 1 6 ∣ 000 ⟩ + 1 3 ∣ 100 ⟩ ) = 2 6 ∣ 000 ⟩ + 2 3 ∣ 100 ⟩ = 1 3 ∣ 000 ⟩ + 2 3 ∣ 100 ⟩ \begin{aligned} |\psi_0\rangle &= \frac{1}{\sqrt{p_0}} \left(\frac{1}{\sqrt{6}}|000\rangle + \frac{1}{\sqrt{3}}|100\rangle\right) \\ &= \frac{1}{\sqrt{1/2}} \left(\frac{1}{\sqrt{6}}|000\rangle + \frac{1}{\sqrt{3}}|100\rangle\right) \\ &= \sqrt{2} \left(\frac{1}{\sqrt{6}}|000\rangle + \frac{1}{\sqrt{3}}|100\rangle\right) \\ &= \frac{\sqrt{2}}{\sqrt{6}}|000\rangle + \frac{\sqrt{2}}{\sqrt{3}}|100\rangle \\ &= \frac{1}{\sqrt{3}}|000\rangle + \frac{\sqrt{2}}{\sqrt{3}}|100\rangle \end{aligned} ∣ ψ 0 ⟩ = p 0 1 ( 6 1 ∣000 ⟩ + 3 1 ∣100 ⟩ ) = 1/2 1 ( 6 1 ∣000 ⟩ + 3 1 ∣100 ⟩ ) = 2 ( 6 1 ∣000 ⟩ + 3 1 ∣100 ⟩ ) = 6 2 ∣000 ⟩ + 3 2 ∣100 ⟩ = 3 1 ∣000 ⟩ + 3 2 ∣100 ⟩
정규화 검증 :
∣ 1 3 ∣ 2 + ∣ 2 3 ∣ 2 = 1 3 + 2 3 = 1 ✓ \left|\frac{1}{\sqrt{3}}\right|^2 + \left|\frac{\sqrt{2}}{\sqrt{3}}\right|^2 = \frac{1}{3} + \frac{2}{3} = 1 \quad \checkmark 3 1 2 + 3 2 2 = 3 1 + 3 2 = 1 ✓
선택지와의 비교 :
∣ ψ 0 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ + 2 ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ 3 |\psi_0\rangle = \frac{|0\rangle|0\rangle|-\rangle + \sqrt{2}|1\rangle|0\rangle|0\rangle}{\sqrt{3}} ∣ ψ 0 ⟩ = 3 ∣0 ⟩ ∣0 ⟩ ∣ − ⟩ + 2 ∣1 ⟩ ∣0 ⟩ ∣0 ⟩
계수 검증 :
∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ |0\rangle|0\rangle|-\rangle ∣0 ⟩ ∣0 ⟩ ∣ − ⟩ 1 3 \frac{1}{\sqrt{3}} 3 1 ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ |1\rangle|0\rangle|0\rangle ∣1 ⟩ ∣0 ⟩ ∣0 ⟩ 2 3 \frac{\sqrt{2}}{\sqrt{3}} 3 2 정규화 확인 :
∣ 1 3 ∣ 2 + ∣ 2 3 ∣ 2 = 1 3 + 2 3 = 1 ✓ \left|\frac{1}{\sqrt{3}}\right|^2 + \left|\frac{\sqrt{2}}{\sqrt{3}}\right|^2 = \frac{1}{3} + \frac{2}{3} = 1 \quad \checkmark 3 1 2 + 3 2 2 = 3 1 + 3 2 = 1 ✓
∣ − ⟩ |-\rangle ∣ − ⟩ ∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ |0\rangle|0\rangle|-\rangle ∣0 ⟩ ∣0 ⟩ ∣ − ⟩
원래 상태에서 ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ + ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) ∣ + ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩)
중요한 통찰 : ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle|+\rangle|0\rangle ∣0 ⟩ ∣ + ⟩ ∣0 ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ 1 ⟩ |0\rangle|+\rangle|1\rangle ∣0 ⟩ ∣ + ⟩ ∣1 ⟩ ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle|+\rangle|0\rangle ∣0 ⟩ ∣ + ⟩ ∣0 ⟩
하지만 다른 가능성 : ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle ∣0 ⟩ ∣ + ⟩ |+\rangle ∣ + ⟩
올바른 해석 : 원래 상태에서 ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩
∣ + ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) ∣ + ⟩ = 2 1 ( ∣0 ⟩ + ∣1 ⟩) ∣ 0 ⟩ ∣ + ⟩ = ∣ 0 ⟩ ⊗ 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = 1 2 ∣ 0 ⟩ ∣ 0 ⟩ + 1 2 ∣ 0 ⟩ ∣ 1 ⟩ |0\rangle|+\rangle = |0\rangle \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = \frac{1}{\sqrt{2}}|0\rangle|0\rangle + \frac{1}{\sqrt{2}}|0\rangle|1\rangle ∣0 ⟩ ∣ + ⟩ = ∣0 ⟩ ⊗ 2 1 ( ∣0 ⟩ + ∣1 ⟩) = 2 1 ∣0 ⟩ ∣0 ⟩ + 2 1 ∣0 ⟩ ∣1 ⟩ 세 번째 qubit이 명시되지 않았으므로, 이것을 ∣ 0 ⟩ ∣ + ⟩ ∣ 0 ⟩ |0\rangle|+\rangle|0\rangle ∣0 ⟩ ∣ + ⟩ ∣0 ⟩
∣ 0 ⟩ ∣ + ⟩ ∣ 0 ⟩ = 1 2 ∣ 0 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ + 1 2 ∣ 0 ⟩ ∣ 1 ⟩ ∣ 0 ⟩ |0\rangle|+\rangle|0\rangle = \frac{1}{\sqrt{2}}|0\rangle|0\rangle|0\rangle + \frac{1}{\sqrt{2}}|0\rangle|1\rangle|0\rangle ∣0 ⟩ ∣ + ⟩ ∣0 ⟩ = 2 1 ∣0 ⟩ ∣0 ⟩ ∣0 ⟩ + 2 1 ∣0 ⟩ ∣1 ⟩ ∣0 ⟩ 중간 qubit(q₁)이 ∣ 0 ⟩ |0\rangle ∣0 ⟩
1 2 ∣ 0 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ \frac{1}{\sqrt{2}}|0\rangle|0\rangle|0\rangle 2 1 ∣0 ⟩ ∣0 ⟩ ∣0 ⟩ 하지만 선택지에서 ∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ |0\rangle|0\rangle|-\rangle ∣0 ⟩ ∣0 ⟩ ∣ − ⟩ ∣ − ⟩ |-\rangle ∣ − ⟩ ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩
재검토 : ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ 0 ⟩ ∣ + ⟩ ∣ − ⟩ |0\rangle|+\rangle|-\rangle ∣0 ⟩ ∣ + ⟩ ∣ − ⟩
최종 해석 : 선택지의 ∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ |0\rangle|0\rangle|-\rangle ∣0 ⟩ ∣0 ⟩ ∣ − ⟩ ∣ 0 ⟩ ∣ + ⟩ |0\rangle|+\rangle ∣0 ⟩ ∣ + ⟩ ∣ − ⟩ |-\rangle ∣ − ⟩ ∣ 000 ⟩ |000\rangle ∣000 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ |0\rangle|0\rangle|0\rangle ∣0 ⟩ ∣0 ⟩ ∣0 ⟩
p 0 = 1 2 , ∣ ψ 0 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ ∣ − ⟩ + 2 ∣ 1 ⟩ ∣ 0 ⟩ ∣ 0 ⟩ 3 p_0 = \frac{1}{2}, \quad |\psi_0\rangle = \frac{|0\rangle|0\rangle|-\rangle + \sqrt{2}|1\rangle|0\rangle|0\rangle}{\sqrt{3}} p 0 = 2 1 , ∣ ψ 0 ⟩ = 3 ∣0 ⟩ ∣0 ⟩ ∣ − ⟩ + 2 ∣1 ⟩ ∣0 ⟩ ∣0 ⟩
중간 qubit에 표준 기저 측정을 수행하면, 중간 qubit이 ∣ 0 ⟩ |0\rangle ∣0 ⟩
Σ = { 0 , 1 , 2 , … , 9 } \Sigma = \{0, 1, 2, \ldots, 9\} Σ = { 0 , 1 , 2 , … , 9 }
A. ( 1 − 2 ) ∣ 7 ⟩ + 2 ∣ 2 ⟩ (1 - \sqrt{2})|7\rangle + \sqrt{2}|2\rangle ( 1 − 2 ) ∣7 ⟩ + 2 ∣2 ⟩ ( 3 / 2 ) ∣ 0 ⟩ + ( 1 / 2 ) ∣ 1 ⟩ − ∣ 0 ⟩ (3/2)|0\rangle + (1/2)|1\rangle - |0\rangle ( 3/2 ) ∣0 ⟩ + ( 1/2 ) ∣1 ⟩ − ∣0 ⟩ ( 1 / 10 ) ∑ j = 1 9 ∣ j ⟩ (1/10) \sum_{j=1}^{9} |j\rangle ( 1/10 ) ∑ j = 1 9 ∣ j ⟩ ( 2 / 5 ) ∣ 8 ⟩ + ( 1 / 5 ) ( ∣ 3 ⟩ + ∣ 4 ⟩ + ∣ 5 ⟩ ) (2/5)|8\rangle + (1/5)(|3\rangle + |4\rangle + |5\rangle) ( 2/5 ) ∣8 ⟩ + ( 1/5 ) ( ∣3 ⟩ + ∣4 ⟩ + ∣5 ⟩) ( 1 / 3 ) ∣ 3 ⟩ + ( 1 / 4 ) ∣ 4 ⟩ + ( 5 / 12 ) ∣ 5 ⟩ (1/3)|3\rangle + (1/4)|4\rangle + (5/12)|5\rangle ( 1/3 ) ∣3 ⟩ + ( 1/4 ) ∣4 ⟩ + ( 5/12 ) ∣5 ⟩
확률 벡터는 다음 두 조건을 만족하는 벡터입니다:
모든 항목은 음이 아닌 실수 : 각 성분이 p i ≥ 0 p_i \geq 0 p i ≥ 0 항목들의 합은 1 : ∑ i p i = 1 \sum_i p_i = 1 ∑ i p i = 1 확률 벡터는 확률적 상태(probabilistic state)를 나타냅니다 각 성분은 해당 고전 상태에 있을 확률을 나타냅니다 모든 확률의 합은 1이어야 합니다 (정규화 조건) 확률 벡터는 ∑ a ∈ Σ p a ∣ a ⟩ \sum_{a \in \Sigma} p_a |a\rangle ∑ a ∈ Σ p a ∣ a ⟩ 여기서 p a ≥ 0 p_a \geq 0 p a ≥ 0 ∑ a ∈ Σ p a = 1 \sum_{a \in \Sigma} p_a = 1 ∑ a ∈ Σ p a = 1 각 선택지를 확인합니다:
계수 확인: 1 − 2 ≈ 1 − 1.414 = − 0.414 < 0 1 - \sqrt{2} \approx 1 - 1.414 = -0.414 < 0 1 − 2 ≈ 1 − 1.414 = − 0.414 < 0 2 ≈ 1.414 > 0 \sqrt{2} \approx 1.414 > 0 2 ≈ 1.414 > 0 합: ( 1 − 2 ) + 2 = 1 (1 - \sqrt{2}) + \sqrt{2} = 1 ( 1 − 2 ) + 2 = 1 결과 : 음수 계수가 있으므로 확률 벡터가 아닙니다 전개: ( 1 / 10 ) ( ∣ 1 ⟩ + ∣ 2 ⟩ + ∣ 3 ⟩ + ∣ 4 ⟩ + ∣ 5 ⟩ + ∣ 6 ⟩ + ∣ 7 ⟩ + ∣ 8 ⟩ + ∣ 9 ⟩ ) (1/10)(|1\rangle + |2\rangle + |3\rangle + |4\rangle + |5\rangle + |6\rangle + |7\rangle + |8\rangle + |9\rangle) ( 1/10 ) ( ∣1 ⟩ + ∣2 ⟩ + ∣3 ⟩ + ∣4 ⟩ + ∣5 ⟩ + ∣6 ⟩ + ∣7 ⟩ + ∣8 ⟩ + ∣9 ⟩) 계수 확인: 각 계수가 1 / 10 ≥ 0 1/10 \geq 0 1/10 ≥ 0 합: 9 × ( 1 / 10 ) = 9 / 10 ≠ 1 9 \times (1/10) = 9/10 \neq 1 9 × ( 1/10 ) = 9/10 = 1 결과 : 합이 1이 아니므로 확률 벡터가 아닙니다 전개: ( 2 / 5 ) ∣ 8 ⟩ + ( 1 / 5 ) ∣ 3 ⟩ + ( 1 / 5 ) ∣ 4 ⟩ + ( 1 / 5 ) ∣ 5 ⟩ (2/5)|8\rangle + (1/5)|3\rangle + (1/5)|4\rangle + (1/5)|5\rangle ( 2/5 ) ∣8 ⟩ + ( 1/5 ) ∣3 ⟩ + ( 1/5 ) ∣4 ⟩ + ( 1/5 ) ∣5 ⟩ 계수 확인: 2 / 5 ≥ 0 2/5 \geq 0 2/5 ≥ 0 1 / 5 ≥ 0 1/5 \geq 0 1/5 ≥ 0 합: 2 / 5 + 1 / 5 + 1 / 5 + 1 / 5 = 5 / 5 = 1 2/5 + 1/5 + 1/5 + 1/5 = 5/5 = 1 2/5 + 1/5 + 1/5 + 1/5 = 5/5 = 1 결과 : 확률 벡터입니다 계수 확인: 1 / 3 ≥ 0 1/3 \geq 0 1/3 ≥ 0 1 / 4 ≥ 0 1/4 \geq 0 1/4 ≥ 0 5 / 12 ≥ 0 5/12 \geq 0 5/12 ≥ 0 합: 1 / 3 + 1 / 4 + 5 / 12 = 4 / 12 + 3 / 12 + 5 / 12 = 12 / 12 = 1 1/3 + 1/4 + 5/12 = 4/12 + 3/12 + 5/12 = 12/12 = 1 1/3 + 1/4 + 5/12 = 4/12 + 3/12 + 5/12 = 12/12 = 1 결과 : 확률 벡터입니다 결과: 선택지 B, D, E가 확률 벡터입니다.
확률 벡터가 되려면 모든 계수가 비음이어야 하고, 계수들의 합이 1이어야 합니다. A는 음수 계수가 있고, C는 합이 1이 아닙니다.
얽힘 상태들의 중첩이 항상 얽힘 상태를 만드는 것은 아닙니다 예: ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ϕ − ⟩ |\phi^-\rangle ∣ ϕ − ⟩ ∣ 00 ⟩ |00\rangle ∣00 ⟩ 복합 시스템의 고전 상태 집합은 **카르테시안 곱(Cartesian product)**입니다 텐서 곱은 벡터나 행렬에 대한 연산이며, 집합에 대해서는 카르테시안 곱을 사용합니다 알려지지 않은 양자 상태를 복제하는 연산은 비선형입니다 ∣ ψ ⟩ ↦ ∣ ψ ⟩ ⊗ ∣ ψ ⟩ |\psi\rangle \mapsto |\psi\rangle \otimes |\psi\rangle ∣ ψ ⟩ ↦ ∣ ψ ⟩ ⊗ ∣ ψ ⟩ 복제 연산은 유니터리 연산으로 표현될 수 없습니다 네 가지 Bell 상태는 두 qubit 공간의 정규 직교 기저를 형성합니다 Bell basis는 완전한 기저입니다 두 유니터리 행렬의 텐서 곱 U ⊗ V U \otimes V U ⊗ V 이는 독립 연산(independent operations)을 의미합니다 얽힌 시스템에서 한 qubit을 측정하면, 측정 후 상태는 product state가 될 수 있습니다 예: ∣ ϕ + ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) ∣ ϕ + ⟩ = 2 1 ( ∣00 ⟩ + ∣11 ⟩) ∣ 00 ⟩ |00\rangle ∣00 ⟩ ∣ 11 ⟩ |11\rangle ∣11 ⟩ 거짓 : 복합 시스템의 고전 상태 집합은 **카르테시안 곱(Cartesian product)**입니다텐서 곱은 벡터나 행렬에 대한 연산이며, 집합에 대해서는 카르테시안 곱 Σ × Γ \Sigma \times \Gamma Σ × Γ 거짓 : 이것은 복제(cloning) 연산으로, 비선형 입니다No-cloning theorem에 의해 알려지지 않은 양자 상태를 복제하는 것은 불가능하며, 복제 연산은 선형이 아닙니다 예: ∣ 0 ⟩ + ∣ 1 ⟩ |0\rangle + |1\rangle ∣0 ⟩ + ∣1 ⟩ ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ + ∣ 11 ⟩ (|0\rangle + |1\rangle) \otimes (|0\rangle + |1\rangle) = |00\rangle + |01\rangle + |10\rangle + |11\rangle ( ∣0 ⟩ + ∣1 ⟩) ⊗ ( ∣0 ⟩ + ∣1 ⟩) = ∣00 ⟩ + ∣01 ⟩ + ∣10 ⟩ + ∣11 ⟩ ∣ 0 ⟩ ⊗ ∣ 0 ⟩ + ∣ 1 ⟩ ⊗ ∣ 1 ⟩ |0\rangle \otimes |0\rangle + |1\rangle \otimes |1\rangle ∣0 ⟩ ⊗ ∣0 ⟩ + ∣1 ⟩ ⊗ ∣1 ⟩ 참 : 네 가지 Bell 상태는 두 qubit 공간의 정규 직교 기저를 형성합니다Bell basis: { ∣ ϕ + ⟩ , ∣ ϕ − ⟩ , ∣ ψ + ⟩ , ∣ ψ − ⟩ } \{|\phi^+\rangle, |\phi^-\rangle, |\psi^+\rangle, |\psi^-\rangle\} { ∣ ϕ + ⟩ , ∣ ϕ − ⟩ , ∣ ψ + ⟩ , ∣ ψ − ⟩} 각 Bell 상태는 정규화되어 있고, 서로 직교합니다 참 : U ⊗ V U \otimes V U ⊗ V 첫 번째 시스템에 U U U V V V 이것은 독립 연산(independent operations)의 정의입니다 거짓 : 얽힌 시스템에서 한 qubit을 측정하면, 측정 후 상태는 product state가 될 수 있습니다예: ∣ ϕ + ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) ∣ ϕ + ⟩ = 2 1 ( ∣00 ⟩ + ∣11 ⟩) 결과 0: ∣ 00 ⟩ |00\rangle ∣00 ⟩ 결과 1: ∣ 11 ⟩ |11\rangle ∣11 ⟩ 측정 후에는 얽힘이 사라집니다 다음 중 존재하는 수학적 객체를 모두 선택하라.
A. A nonzero vector ∣ ψ ⟩ |\psi\rangle ∣ ψ ⟩ ⟨ ψ ∣ ψ ⟩ = 0 \langle\psi|\psi\rangle = 0 ⟨ ψ ∣ ψ ⟩ = 0
유니터리 행렬 : U † U = I U^\dagger U = I U † U = I 확률 행렬(Stochastic matrix) : 모든 항목이 비음: M i j ≥ 0 M_{ij} \geq 0 M ij ≥ 0 각 열의 합이 1: ∑ i M i j = 1 \sum_i M_{ij} = 1 ∑ i M ij = 1 순열 행렬(Permutation matrix) : 각 행과 열에 정확히 하나의 1이 있고 나머지는 0인 행렬유니터리 행렬이 확률 행렬이려면, 각 열이 확률 벡터이면서 동시에 정규 직교 기저를 형성해야 합니다 이는 순열 행렬만 가능합니다 (각 열에 정확히 하나의 1이 있고 나머지는 0) 에르미트 행렬 : H † = H H^\dagger = H H † = H 유니터리 행렬 : U † U = I U^\dagger U = I U † U = I 유니터리이면서 에르미트인 행렬은 U † = U U^\dagger = U U † = U U † U = I U^\dagger U = I U † U = I U 2 = I U^2 = I U 2 = I 예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) 사영 행렬 : P 2 = P P^2 = P P 2 = P P † = P P^\dagger = P P † = P 사영 행렬의 고유값은 0 또는 1만 가질 수 있습니다 유니터리 사영 행렬 : P 2 = P P^2 = P P 2 = P P † P = I P^\dagger P = I P † P = I P 2 = P P^2 = P P 2 = P P † P = I P^\dagger P = I P † P = I P = I P = I P = I 따라서 유니터리 사영 행렬은 단위 행렬뿐입니다 모든 사영 행렬은 에르미트입니다 (P † = P P^\dagger = P P † = P 하지만 모든 에르미트 행렬이 사영 행렬인 것은 아닙니다 예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) Z 2 = I ≠ Z Z^2 = I \neq Z Z 2 = I = Z 유니터리 연산은 선형 연산 입니다 모든 양자 상태 벡터를 같은 상태로 매핑하는 연산은 선형이 아닙니다 예: U ∣ ψ ⟩ = ∣ 00 ⟩ U|\psi\rangle = |00\rangle U ∣ ψ ⟩ = ∣00 ⟩ ∣ ψ ⟩ |\psi\rangle ∣ ψ ⟩ U ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = ∣ 00 ⟩ U(|0\rangle + |1\rangle) = |00\rangle U ( ∣0 ⟩ + ∣1 ⟩) = ∣00 ⟩ U ∣ 0 ⟩ + U ∣ 1 ⟩ = ∣ 00 ⟩ + ∣ 00 ⟩ = 2 ∣ 00 ⟩ U|0\rangle + U|1\rangle = |00\rangle + |00\rangle = 2|00\rangle U ∣0 ⟩ + U ∣1 ⟩ = ∣00 ⟩ + ∣00 ⟩ = 2∣00 ⟩ 존재하지 않음 ⟨ ψ ∣ ψ ⟩ = 0 \langle\psi|\psi\rangle = 0 ⟨ ψ ∣ ψ ⟩ = 0 ∥ ∣ ψ ⟩ ∥ 2 = 0 \||\psi\rangle\|^2 = 0 ∥∣ ψ ⟩ ∥ 2 = 0 ∥ ∣ ψ ⟩ ∥ = 0 \||\psi\rangle\| = 0 ∥∣ ψ ⟩ ∥ = 0 노름이 0인 벡터는 영벡터뿐입니다 따라서 0이 아닌 벡터에 대해 ⟨ ψ ∣ ψ ⟩ = 0 \langle\psi|\psi\rangle = 0 ⟨ ψ ∣ ψ ⟩ = 0 존재하지 않음 유니터리 행렬이 확률 행렬이려면, 각 열이 확률 벡터이면서 동시에 정규 직교 기저를 형성해야 합니다 각 열에 정확히 하나의 1이 있고 나머지는 0인 경우만 가능합니다 이것은 순열 행렬의 정의입니다 따라서 유니터리이면서 확률 행렬인 행렬은 순열 행렬뿐입니다 존재함 예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) Z † = Z Z^\dagger = Z Z † = Z Z † Z = Z 2 = I Z^\dagger Z = Z^2 = I Z † Z = Z 2 = I Z ≠ I Z \neq I Z = I 다른 예: Pauli-X, Pauli-Y 행렬도 유니터리이면서 에르미트입니다 주의 : 문제에서 선택지 C와 E가 동일한 텍스트를 가지고 있습니다. 이것은 문제의 오류일 수도 있지만, 실제로는 다른 의미일 수도 있습니다.
가능한 해석 1 : E가 C와 동일하다면, C와 마찬가지로 존재함 입니다.
예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) Z † = Z Z^\dagger = Z Z † = Z Z † Z = Z 2 = I Z^\dagger Z = Z^2 = I Z † Z = Z 2 = I Z ≠ I Z \neq I Z = I 가능한 해석 2 : E가 "A Hermitian matrix that is not a projection matrix."를 의미한다면, 존재함 입니다.
예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) Z † = Z Z^\dagger = Z Z † = Z Z 2 = I ≠ Z Z^2 = I \neq Z Z 2 = I = Z 다른 예: 모든 대각 행렬이 에르미트이지만, 고유값이 0 또는 1이 아닌 경우 사영 행렬이 아닙니다 현재 해석 : 문제의 텍스트를 그대로 따르면, E는 C와 동일하므로 존재함 입니다.
존재하지 않음 모든 양자 상태 벡터를 같은 상태 ∣ 00 ⟩ |00\rangle ∣00 ⟩ 선형이 아닙니다 유니터리 연산은 선형 연산이어야 합니다 반례: U ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = ∣ 00 ⟩ U(|0\rangle + |1\rangle) = |00\rangle U ( ∣0 ⟩ + ∣1 ⟩) = ∣00 ⟩ U ∣ 0 ⟩ + U ∣ 1 ⟩ = ∣ 00 ⟩ + ∣ 00 ⟩ = 2 ∣ 00 ⟩ U|0\rangle + U|1\rangle = |00\rangle + |00\rangle = 2|00\rangle U ∣0 ⟩ + U ∣1 ⟩ = ∣00 ⟩ + ∣00 ⟩ = 2∣00 ⟩ 따라서 모든 상태를 같은 상태로 매핑하는 유니터리 연산은 존재하지 않습니다 A: 내적이 0인 0이 아닌 벡터는 존재하지 않습니다 (노름이 0이면 영벡터뿐) B: 유니터리이면서 확률 행렬인 행렬은 순열 행렬뿐입니다 C : 유니터리이면서 에르미트이지만 단위 행렬이 아닌 행렬 (예: Pauli-Z) - 존재함 D: 유니터리 사영 행렬은 단위 행렬뿐입니다 (단위 행렬 제외하면 존재하지 않음) E : 문제에서 C와 동일한 텍스트이지만, "사영 행렬이 아닌 에르미트 행렬"로 해석하면 존재함 (예: Pauli-Z) - 존재함 F: 모든 상태를 같은 상태로 매핑하는 유니터리 연산은 선형이 아니므로 존재하지 않습니다 결과: 선택지 C, E가 존재하는 수학적 객체입니다.
C : 유니터리이면서 에르미트이지만 단위 행렬이 아닌 행렬 (예: Pauli-Z 행렬 Z = ( 1 0 0 − 1 ) Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} Z = ( 1 0 0 − 1 ) E : 문제의 텍스트가 C와 동일하지만, "사영 행렬이 아닌 에르미트 행렬"로 해석하면 존재함 (예: Pauli-Z 행렬)다른 선택지들은 존재하지 않습니다:
A : 내적이 0인 0이 아닌 벡터는 존재하지 않습니다 (노름이 0이면 영벡터뿐)B : 유니터리이면서 확률 행렬인 행렬은 순열 행렬뿐입니다D : 유니터리 사영 행렬은 단위 행렬뿐입니다 (단위 행렬 제외하면 존재하지 않음)F : 모든 상태를 같은 상태로 매핑하는 유니터리 연산은 선형이 아니므로 존재하지 않습니다"Entanglement in Action" 강의에서 다룬 프로토콜의 맥락에서 e-bit을 정확히 설명하는 문장을 모두 선택하라.
e-bit : 얽힘(entanglement)의 한 단위를 나타내는 리소스물리적 표현 : Bell 상태 ∣ ϕ + ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ |\phi^+\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle ∣ ϕ + ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩ e-bit은 두 qubit의 물리적 상태이지만, 얽힘의 양은 1 e-bit입니다 Alice와 Bob이 e-bit을 공유한다는 것은: Alice가 qubit A를 가지고 있음 Bob이 qubit B를 가지고 있음 함께 쌍 ( A , B ) (A, B) ( A , B ) ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ e-bit은 두 당사자(Alice와 Bob) 사이에 공유되는 리소스입니다 e-bit은 양자 프로토콜에서 리소스로 사용됩니다 양자 텔레포테이션 : 1 e-bit과 2 비트의 고전 통신을 사용하여 1 qubit을 전송초밀도 코딩 : 1 e-bit과 1 qubit의 양자 통신을 사용하여 2 비트의 고전 정보를 전송프로토콜이 완료되면 e-bit은 소비되어 더 이상 사용할 수 없습니다 e-bit은 단일 qubit이 아닙니다 e-bit은 두 qubit의 얽힘 상태입니다 e-bit은 특정 Bell 상태 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ e-bit 자체가 qubit을 즉시 전송하는 것은 아닙니다 e-bit은 프로토콜에서 리소스로 사용되지만, qubit 전송을 위해서는 추가적인 연산과 고전 통신이 필요합니다 예: 양자 텔레포테이션에서 e-bit과 고전 통신을 함께 사용하여 qubit을 전송합니다 각 선택지를 확인합니다:
참 : e-bit은 두 당사자(Alice와 Bob) 사이에 공유됩니다Alice가 qubit A를 가지고 있고, Bob이 qubit B를 가지고 있으며, 함께 쌍 ( A , B ) (A, B) ( A , B ) ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 양자 텔레포테이션, 초밀도 코딩, CHSH 게임 등 모든 프로토콜에서 e-bit은 Alice와 Bob 사이에 공유됩니다 거짓 : e-bit은 단일 qubit이 아닙니다e-bit은 두 qubit의 얽힘 상태입니다 구체적으로, Bell 상태 ∣ ϕ + ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ |\phi^+\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle ∣ ϕ + ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩ 따라서 e-bit은 두 qubit 시스템의 상태입니다 참 : e-bit은 프로토콜에서 소비되는 리소스입니다양자 텔레포테이션 : 1 e-bit과 2 비트의 고전 통신을 사용하여 1 qubit을 전송 (e-bit 소비)초밀도 코딩 : 1 e-bit과 1 qubit의 양자 통신을 사용하여 2 비트의 고전 정보를 전송 (e-bit 소비)프로토콜이 완료되면 e-bit은 소비되어 더 이상 사용할 수 없습니다 거짓 : e-bit 자체가 qubit을 즉시 전송하는 것은 아닙니다e-bit은 프로토콜에서 리소스로 사용되지만, qubit 전송을 위해서는 추가적인 연산과 고전 통신이 필요합니다 예: 양자 텔레포테이션에서 e-bit과 함께 측정과 고전 통신이 필요합니다 e-bit만으로는 qubit을 전송할 수 없습니다 참 : e-bit은 특정 Bell 상태 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 정의에 따르면, Bell 상태 ∣ ϕ + ⟩ = 1 2 ∣ 00 ⟩ + 1 2 ∣ 11 ⟩ |\phi^+\rangle = \frac{1}{\sqrt{2}}|00\rangle + \frac{1}{\sqrt{2}}|11\rangle ∣ ϕ + ⟩ = 2 1 ∣00 ⟩ + 2 1 ∣11 ⟩ 다른 Bell 상태들(∣ ϕ − ⟩ |\phi^-\rangle ∣ ϕ − ⟩ ∣ ψ + ⟩ |\psi^+\rangle ∣ ψ + ⟩ ∣ ψ − ⟩ |\psi^-\rangle ∣ ψ − ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 결과: 가정 B, D, F가 참입니다.
B : e-bit은 두 당사자(Alice와 Bob) 사이에 공유됩니다D : e-bit은 프로토콜에서 소비되는 리소스입니다F : e-bit은 특정 Bell 상태 ∣ ϕ + ⟩ |\phi^+\rangle ∣ ϕ + ⟩ 다른 가정들은 오류 입니다.:
A : e-bit은 생성할 수 있습니다 (Hadamard + CNOT로 준비 가능)C : e-bit은 단일 qubit이 아니라 두 qubit의 얽힘 상태입니다E : e-bit 자체가 qubit을 즉시 전송하는 것은 아니며, 추가 연산과 통신이 필요합니다다음은 모두 3 × 3 행렬입니다. 확률 행렬(stochastic matrix)인 것을 모두 선택하라.
선택지 A. ∣ 0 ⟩ ⟨ 0 ∣ + ∣ 1 ⟩ ⟨ 1 ∣ − ∣ 2 ⟩ ⟨ 2 ∣ |0\rangle\langle0| + |1\rangle\langle1| - |2\rangle\langle2| ∣0 ⟩ ⟨ 0∣ + ∣1 ⟩ ⟨ 1∣ − ∣2 ⟩ ⟨ 2∣ 선택지 B. ( 0 1 0 0 0 1 1 0 0 ) \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} 0 0 1 1 0 0 0 1 0 선택지 C. ( 1 1 0 0 0 1 0 0 0 ) \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix} 1 0 0 1 0 0 0 1 0 선택지 D. ( 1 / 3 1 / 3 1 / 3 1 / 4 5 / 12 1 / 3 5 / 12 1 / 3 1 / 4 ) \begin{pmatrix} 1/3 & 1/3 & 1/3 \\ 1/4 & 5/12 & 1/3 \\ 5/12 & 1/3 & 1/4 \end{pmatrix} 1/3 1/4 5/12 1/3 5/12 1/3 1/3 1/3 1/4 선택지 E. 1 3 ( ∣ 0 ⟩ + ∣ 1 ⟩ + ∣ 2 ⟩ ) ( ⟨ 0 ∣ + ⟨ 1 ∣ + ⟨ 2 ∣ ) \frac{1}{3}(|0\rangle + |1\rangle + |2\rangle)(\langle0| + \langle1| + \langle2|) 3 1 ( ∣0 ⟩ + ∣1 ⟩ + ∣2 ⟩) (⟨ 0∣ + ⟨ 1∣ + ⟨ 2∣ ) 확률 행렬 : 다음 두 조건을 만족하는 행렬 모든 항목은 음이 아닌 실수입니다 (M i j ≥ 0 M_{ij} \geq 0 M ij ≥ 0 모든 열의 항목들의 합은 1입니다 (∑ i M i j = 1 \sum_i M_{ij} = 1 ∑ i M ij = 1 확률 벡터를 확률 벡터로 매핑합니다 각 열은 확률 벡터를 나타냅니다 ∣ i ⟩ ⟨ j ∣ |i\rangle\langle j| ∣ i ⟩ ⟨ j ∣ ( i , j ) (i,j) ( i , j ) ∣ i ⟩ ⟨ i ∣ |i\rangle\langle i| ∣ i ⟩ ⟨ i ∣ i i i 1 3 ( ∣ 0 ⟩ + ∣ 1 ⟩ + ∣ 2 ⟩ ) ( ⟨ 0 ∣ + ⟨ 1 ∣ + ⟨ 2 ∣ ) \frac{1}{3}(|0\rangle + |1\rangle + |2\rangle)(\langle0| + \langle1| + \langle2|) 3 1 ( ∣0 ⟩ + ∣1 ⟩ + ∣2 ⟩) (⟨ 0∣ + ⟨ 1∣ + ⟨ 2∣ ) 1 3 \frac{1}{3} 3 1 각 행과 열에 정확히 하나의 1이 있고 나머지는 0인 행렬 순열 행렬은 확률 행렬의 특수한 경우입니다 각 선택지를 확인합니다:
비음 조건 확인 : 모든 항목이 0 또는 1이므로 비음입니다 ✓열의 합 확인 : 첫 번째 열: 0 + 0 + 1 = 1 0 + 0 + 1 = 1 0 + 0 + 1 = 1 두 번째 열: 1 + 0 + 0 = 1 1 + 0 + 0 = 1 1 + 0 + 0 = 1 세 번째 열: 0 + 1 + 0 = 1 0 + 1 + 0 = 1 0 + 1 + 0 = 1 따라서 확률 행렬입니다 비음 조건 확인 : 모든 항목이 0 또는 1이므로 비음입니다 ✓열의 합 확인 : 첫 번째 열: 1 + 0 + 0 = 1 1 + 0 + 0 = 1 1 + 0 + 0 = 1 두 번째 열: 1 + 0 + 0 = 1 1 + 0 + 0 = 1 1 + 0 + 0 = 1 세 번째 열: 0 + 1 + 0 = 1 0 + 1 + 0 = 1 0 + 1 + 0 = 1 따라서 확률 행렬입니다 비음 조건 확인 : 모든 항목이 양수이므로 비음입니다 ✓열의 합 확인 : 첫 번째 열: 1 3 + 1 4 + 5 12 = 4 12 + 3 12 + 5 12 = 12 12 = 1 \frac{1}{3} + \frac{1}{4} + \frac{5}{12} = \frac{4}{12} + \frac{3}{12} + \frac{5}{12} = \frac{12}{12} = 1 3 1 + 4 1 + 12 5 = 12 4 + 12 3 + 12 5 = 12 12 = 1 두 번째 열: 1 3 + 5 12 + 1 3 = 4 12 + 5 12 + 4 12 = 13 12 ≠ 1 \frac{1}{3} + \frac{5}{12} + \frac{1}{3} = \frac{4}{12} + \frac{5}{12} + \frac{4}{12} = \frac{13}{12} \neq 1 3 1 + 12 5 + 3 1 = 12 4 + 12 5 + 12 4 = 12 13 = 1 세 번째 열: 1 3 + 1 3 + 1 4 = 4 12 + 4 12 + 3 12 = 11 12 ≠ 1 \frac{1}{3} + \frac{1}{3} + \frac{1}{4} = \frac{4}{12} + \frac{4}{12} + \frac{3}{12} = \frac{11}{12} \neq 1 3 1 + 3 1 + 4 1 = 12 4 + 12 4 + 12 3 = 12 11 = 1 두 번째와 세 번째 열의 합이 1이 아니므로 확률 행렬이 아닙니다 결과: 선택지 B, C, E가 확률 행렬입니다.
B : 순열 행렬로, 모든 열의 합이 1이고 모든 항목이 비음입니다C : 모든 열의 합이 1이고 모든 항목이 비음입니다E : 균등 행렬로, 모든 원소가 1 3 \frac{1}{3} 3 1 다른 선택지들은 확률 행렬이 아닙니다:
A : 세 번째 대각 원소가 − 1 -1 − 1 D : 두 번째와 세 번째 열의 합이 1이 아닙니다고전 상태 집합이 Σ = { # , b , ♮ } \Sigma = \{\#, b, \natural\} Σ = { # , b , ♮ }
선택지 A. i − 3 2 3 ∣ ♮ ⟩ − 1 − i 12 ∣ b ⟩ + 1 2 ∣ # ⟩ \frac{i-\sqrt{3}}{2\sqrt{3}}|\natural\rangle - \frac{1-i}{\sqrt{12}}|b\rangle + \frac{1}{\sqrt{2}}|\#\rangle 2 3 i − 3 ∣♮ ⟩ − 12 1 − i ∣ b ⟩ + 2 1 ∣# ⟩ 선택지 B. 1 2 ( 6 ∣ # ⟩ − 2 ∣ b ⟩ + 2 i ∣ ♮ ⟩ ) \frac{1}{2}(\sqrt{6}|\#\rangle - \sqrt{2}|b\rangle + 2i|\natural\rangle) 2 1 ( 6 ∣# ⟩ − 2 ∣ b ⟩ + 2 i ∣♮ ⟩) 선택지 C. i 3 ∣ ♮ ⟩ + 1 2 ∣ # ⟩ − 1 6 ∣ b ⟩ \frac{i}{\sqrt{3}}|\natural\rangle + \frac{1}{\sqrt{2}}|\#\rangle - \frac{1}{\sqrt{6}}|b\rangle 3 i ∣♮ ⟩ + 2 1 ∣# ⟩ − 6 1 ∣ b ⟩ 선택지 D. 6 ∣ # ⟩ − 2 ∣ b ⟩ + 2 i ∣ ♮ ⟩ 6 − 2 + 2 i \frac{\sqrt{6}|\#\rangle - \sqrt{2}|b\rangle + 2i|\natural\rangle}{\sqrt{6}-\sqrt{2}+2i} 6 − 2 + 2 i 6 ∣# ⟩ − 2 ∣ b ⟩ + 2 i ∣♮ ⟩ 선택지 E. 1 3 ( ∣ ♮ ⟩ + ∣ b ⟩ + ∣ # ⟩ ) ( ⟨ ♮ ∣ + ⟨ b ∣ + ⟨ # ∣ ) \frac{1}{3}(|\natural\rangle + |b\rangle + |\#\rangle)(\langle\natural| + \langle b| + \langle\#|) 3 1 ( ∣♮ ⟩ + ∣ b ⟩ + ∣# ⟩) (⟨ ♮∣ + ⟨ b ∣ + ⟨ #∣ ) 벡터 ∣ ϕ ⟩ |\phi\rangle ∣ ϕ ⟩ N N N 1 N ∣ ϕ ⟩ \frac{1}{\sqrt{N}}|\phi\rangle N 1 ∣ ϕ ⟩ 벡터 ∣ ϕ ⟩ |\phi\rangle ∣ ϕ ⟩ N N N c c c c ∣ ϕ ⟩ c|\phi\rangle c ∣ ϕ ⟩ ∣ c ∣ 2 N |c|^2 N ∣ c ∣ 2 N 각 선택지를 확인합니다:
내부 벡터 ∣ ϕ ⟩ = 6 ∣ # ⟩ − 2 ∣ b ⟩ + 2 i ∣ ♮ ⟩ |\phi\rangle = \sqrt{6}|\#\rangle - \sqrt{2}|b\rangle + 2i|\natural\rangle ∣ ϕ ⟩ = 6 ∣# ⟩ − 2 ∣ b ⟩ + 2 i ∣♮ ⟩ ∥ ∣ ϕ ⟩ ∥ 2 = ( 6 ) 2 + ( − 2 ) 2 + ∣ 2 i ∣ 2 = 6 + 2 + 4 = 12 \||\phi\rangle\|^2 = (\sqrt{6})^2 + (-\sqrt{2})^2 + |2i|^2 = 6 + 2 + 4 = 12 ∥∣ ϕ ⟩ ∥ 2 = ( 6 ) 2 + ( − 2 ) 2 + ∣2 i ∣ 2 = 6 + 2 + 4 = 12
주어진 벡터는 1 2 ∣ ϕ ⟩ \frac{1}{2}|\phi\rangle 2 1 ∣ ϕ ⟩ ∥ 1 2 ∣ ϕ ⟩ ∥ 2 = ( 1 2 ) 2 ⋅ 12 = 1 4 ⋅ 12 = 3 ≠ 1 \left\|\frac{1}{2}|\phi\rangle\right\|^2 = \left(\frac{1}{2}\right)^2 \cdot 12 = \frac{1}{4} \cdot 12 = 3 \neq 1 2 1 ∣ ϕ ⟩ 2 = ( 2 1 ) 2 ⋅ 12 = 4 1 ⋅ 12 = 3 = 1
따라서 양자 상태 벡터가 아닙니다 내부 벡터 ∣ ϕ ⟩ = 2 ∣ ♮ ⟩ − 2 3 ∣ # ⟩ + 2 i 3 ∣ b ⟩ |\phi\rangle = \sqrt{2}|\natural\rangle - \sqrt{\frac{2}{3}}|\#\rangle + \frac{2i}{\sqrt{3}}|b\rangle ∣ ϕ ⟩ = 2 ∣♮ ⟩ − 3 2 ∣# ⟩ + 3 2 i ∣ b ⟩ ∥ ∣ ϕ ⟩ ∥ 2 = ( 2 ) 2 + ( − 2 3 ) 2 + ∣ 2 i 3 ∣ 2 = 2 + 2 3 + 4 3 = 2 + 6 3 = 2 + 2 = 4 \begin{aligned} \||\phi\rangle\|^2 &= (\sqrt{2})^2 + \left(-\sqrt{\frac{2}{3}}\right)^2 + \left|\frac{2i}{\sqrt{3}}\right|^2 \\ &= 2 + \frac{2}{3} + \frac{4}{3} = 2 + \frac{6}{3} = 2 + 2 = 4 \end{aligned} ∥∣ ϕ ⟩ ∥ 2 = ( 2 ) 2 + ( − 3 2 ) 2 + 3 2 i 2 = 2 + 3 2 + 3 4 = 2 + 3 6 = 2 + 2 = 4
주어진 벡터는 1 2 ∣ ϕ ⟩ \frac{1}{2}|\phi\rangle 2 1 ∣ ϕ ⟩ ∥ 1 2 ∣ ϕ ⟩ ∥ 2 = ( 1 2 ) 2 ⋅ 4 = 1 4 ⋅ 4 = 1 \left\|\frac{1}{2}|\phi\rangle\right\|^2 = \left(\frac{1}{2}\right)^2 \cdot 4 = \frac{1}{4} \cdot 4 = 1 2 1 ∣ ϕ ⟩ 2 = ( 2 1 ) 2 ⋅ 4 = 4 1 ⋅ 4 = 1
따라서 양자 상태 벡터입니다 결과: 선택지 A, C, E가 양자 상태 벡터입니다.
A : 계수들의 절댓값 제곱의 합이 1입니다 (1 3 + 1 6 + 1 2 = 1 \frac{1}{3} + \frac{1}{6} + \frac{1}{2} = 1 3 1 + 6 1 + 2 1 = 1 C : 계수들의 절댓값 제곱의 합이 1입니다 (1 3 + 1 2 + 1 6 = 1 \frac{1}{3} + \frac{1}{2} + \frac{1}{6} = 1 3 1 + 2 1 + 6 1 = 1 E : 내부 벡터의 노름 제곱이 4이고, 1 2 \frac{1}{2} 2 1 다른 선택지들은 양자 상태 벡터가 아닙니다:
B : 내부 벡터의 노름 제곱이 12이고, 1 2 \frac{1}{2} 2 1 D : 분모가 복소수이며, 분자의 노름과 일치하지 않습니다두 유니터리 행렬의 합은 일반적으로 유니터리가 아닙니다 예: I + I = 2 I I + I = 2I I + I = 2 I ( 2 I ) † ( 2 I ) = 4 I ≠ I (2I)^\dagger(2I) = 4I \neq I ( 2 I ) † ( 2 I ) = 4 I = I 유니터리 행렬의 합은 유니터리 조건을 만족하지 않습니다 모든 확률 행렬이 가역인 것은 아닙니다 예: ( 1 1 0 0 ) \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} ( 1 0 1 0 ) 확률 행렬은 모든 열의 합이 1이지만, 이는 가역성을 보장하지 않습니다 확률 행렬은 모든 열이 확률 벡터를 형성하는 행렬입니다 모든 표준 기저 벡터를 확률 벡터로 변환하는 행렬은 확률 행렬입니다 확률 벡터를 항상 확률 벡터로 매핑하는 행렬은 확률 행렬입니다 모든 유니터리 행렬은 가역입니다 유니터리 행렬 U U U U † U = I U^\dagger U = I U † U = I U − 1 = U † U^{-1} = U^\dagger U − 1 = U † 따라서 모든 유니터리 행렬은 역행렬을 가집니다 양자 상태 벡터: 계수들의 절댓값 제곱의 합이 1인 벡터 확률 벡터: 모든 계수가 비음이고 합이 1인 벡터 양자 상태 벡터이면서 확률 벡터인 벡터는 표준 기저 벡터뿐입니다 예: 1 2 ∣ 0 ⟩ + 1 2 ∣ 1 ⟩ \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle 2 1 ∣0 ⟩ + 2 1 ∣1 ⟩ 모든 표준 기저 벡터를 양자 상태 벡터로 변환하는 행렬은 유니터리 행렬입니다 표준 기저 벡터는 정규 직교 기저를 형성하므로, 이를 양자 상태 벡터(노름 1)로 변환하는 행렬은 정규 직교 기저를 정규 직교 기저로 보존합니다 이것은 유니터리 행렬의 정의입니다 참 : 유니터리 연산의 합성은 행렬 곱셈으로 표현됩니다두 유니터리 행렬 U U U V V V U V UV U V 양자 회로에서 여러 게이트를 순차적으로 적용하는 것은 행렬 곱셈에 해당합니다 거짓 : 두 유니터리 행렬의 합은 일반적으로 유니터리가 아닙니다반례: I + I = 2 I I + I = 2I I + I = 2 I ( 2 I ) † ( 2 I ) = 4 I ≠ I (2I)^\dagger(2I) = 4I \neq I ( 2 I ) † ( 2 I ) = 4 I = I 유니터리 행렬의 합은 유니터리 조건을 만족하지 않습니다 거짓 : 모든 확률 행렬이 가역인 것은 아닙니다반례: ( 1 1 0 0 ) \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} ( 1 0 1 0 ) 확률 행렬은 모든 열의 합이 1이지만, 이는 가역성을 보장하지 않습니다 거짓 : 확률은 계수의 절댓값 제곱 ∣ α ∣ 2 |\alpha|^2 ∣ α ∣ 2 절댓값의 제곱근이 아닙니다 올바른 공식: Pr ( a ) = ∣ ⟨ a ∣ ψ ⟩ ∣ 2 \text{Pr}(a) = |\langle a | \psi \rangle|^2 Pr ( a ) = ∣ ⟨ a ∣ ψ ⟩ ∣ 2 참 : 모든 표준 기저 벡터를 확률 벡터로 변환하는 행렬은 확률 행렬입니다확률 행렬의 정의는 모든 열이 확률 벡터를 형성하는 행렬입니다 표준 기저 벡터는 각 열에 해당하므로, 이를 확률 벡터로 변환하는 행렬은 확률 행렬입니다 참 : 모든 유니터리 행렬은 가역입니다유니터리 행렬 U U U U † U = I U^\dagger U = I U † U = I U − 1 = U † U^{-1} = U^\dagger U − 1 = U † 따라서 모든 유니터리 행렬은 역행렬을 가집니다 참 : 양자 상태 벡터이면서 확률 벡터인 벡터는 표준 기저 벡터뿐입니다양자 상태 벡터: 계수들의 절댓값 제곱의 합이 1 확률 벡터: 모든 계수가 비음이고 합이 1 두 조건을 동시에 만족하려면, 하나의 계수만 1이고 나머지는 0이어야 합니다 이것은 표준 기저 벡터의 정의입니다 참 : 모든 표준 기저 벡터를 양자 상태 벡터(노름 1)로 변환하는 행렬은 유니터리 행렬입니다표준 기저 벡터는 정규 직교 기저를 형성하므로, 이를 양자 상태 벡터(노름 1)로 변환하는 행렬은 정규 직교 기저를 정규 직교 기저로 보존합니다 이것은 유니터리 행렬의 정의입니다 (U † U = I U^\dagger U = I U † U = I 결과: 가정 A, E, F, G, H가 참입니다.
A : 유니터리 연산의 합성은 행렬 곱셈으로 표현됩니다E : 모든 표준 기저 벡터를 확률 벡터로 변환하는 행렬은 확률 행렬입니다F : 모든 유니터리 행렬은 가역입니다 (U − 1 = U † U^{-1} = U^\dagger U − 1 = U † G : 양자 상태 벡터이면서 확률 벡터인 벡터는 표준 기저 벡터뿐입니다H : 모든 표준 기저 벡터를 양자 상태 벡터로 변환하는 행렬은 유니터리 행렬입니다다른 가정들은 거짓입니다:
B : 두 유니터리 행렬의 합은 일반적으로 유니터리가 아닙니다C : 모든 확률 행렬이 가역인 것은 아닙니다D : 확률은 계수의 절댓값 제곱이지, 절댓값의 제곱근이 아닙니다다음은 한 쌍의 시스템의 양자 상태 벡터들이다. 각 시스템의 고전 상태 집합은 Σ = { a , b , c } \Sigma = \{a, b, c\} Σ = { a , b , c }
선택지 A. 1 6 ( ∣ a b ⟩ + 2 ∣ a a ⟩ + 2 ∣ c b ⟩ + ∣ b c ⟩ − 2 ∣ b a ⟩ − 2 ∣ c c ⟩ − ∣ a c ⟩ − ∣ b b ⟩ + 4 ∣ c a ⟩ ) \frac{1}{6}(|ab\rangle + 2|aa\rangle + 2|cb\rangle + |bc\rangle - 2|ba\rangle - 2|cc\rangle - |ac\rangle - |bb\rangle + 4|ca\rangle) 6 1 ( ∣ ab ⟩ + 2∣ aa ⟩ + 2∣ c b ⟩ + ∣ b c ⟩ − 2∣ ba ⟩ − 2∣ cc ⟩ − ∣ a c ⟩ − ∣ bb ⟩ + 4∣ c a ⟩) 선택지 B. 1 6 ( ∣ a b ⟩ − 2 ∣ a a ⟩ + 2 ∣ c b ⟩ − ∣ b c ⟩ − 2 ∣ b a ⟩ − 2 ∣ c c ⟩ − ∣ a c ⟩ − ∣ b b ⟩ + 4 ∣ c a ⟩ ) \frac{1}{6}(|ab\rangle - 2|aa\rangle + 2|cb\rangle - |bc\rangle - 2|ba\rangle - 2|cc\rangle - |ac\rangle - |bb\rangle + 4|ca\rangle) 6 1 ( ∣ ab ⟩ − 2∣ aa ⟩ + 2∣ c b ⟩ − ∣ b c ⟩ − 2∣ ba ⟩ − 2∣ cc ⟩ − ∣ a c ⟩ − ∣ bb ⟩ + 4∣ c a ⟩) 선택지 C. 1 2 ( ∣ a ⟩ ∣ b ⟩ + ∣ c ⟩ ∣ b ⟩ ) \frac{1}{\sqrt{2}}(|a\rangle|b\rangle + |c\rangle|b\rangle) 2 1 ( ∣ a ⟩ ∣ b ⟩ + ∣ c ⟩ ∣ b ⟩) 선택지 D. 1 33 ∣ a a ⟩ − 4 33 ∣ a c ⟩ + 4 33 ∣ c a ⟩ \frac{1}{\sqrt{33}}|aa\rangle - \frac{4}{\sqrt{33}}|ac\rangle + \frac{4}{\sqrt{33}}|ca\rangle 33 1 ∣ aa ⟩ − 33 4 ∣ a c ⟩ + 33 4 ∣ c a ⟩ 선택지 E. 1 2 ( ∣ a a ⟩ − ∣ a b ⟩ + ∣ b a ⟩ + ∣ b b ⟩ ) \frac{1}{2}(|aa\rangle - |ab\rangle + |ba\rangle + |bb\rangle) 2 1 ( ∣ aa ⟩ − ∣ ab ⟩ + ∣ ba ⟩ + ∣ bb ⟩) 선택지 F. 1 10 ( ∣ a ⟩ + ∣ c ⟩ ) ⊗ ( ∣ c ⟩ − 4 ∣ b ⟩ ) \frac{1}{\sqrt{10}}(|a\rangle + |c\rangle) \otimes (|c\rangle - 4|b\rangle) 10 1 ( ∣ a ⟩ + ∣ c ⟩) ⊗ ( ∣ c ⟩ − 4∣ b ⟩) Entangled state는 product state가 아닌 상태입니다 즉, ∣ ϕ ⟩ ⊗ ∣ ψ ⟩ |\phi\rangle \otimes |\psi\rangle ∣ ϕ ⟩ ⊗ ∣ ψ ⟩ 얽힌 상태는 두 시스템 간의 상관관계를 나타냅니다 상태 ∣ Ψ ⟩ = ∑ i , j c i j ∣ i j ⟩ |\Psi\rangle = \sum_{i,j} c_{ij}|ij\rangle ∣Ψ ⟩ = ∑ i , j c ij ∣ ij ⟩ ∣ ϕ ⟩ = ∑ i α i ∣ i ⟩ |\phi\rangle = \sum_i \alpha_i|i\rangle ∣ ϕ ⟩ = ∑ i α i ∣ i ⟩ ∣ ψ ⟩ = ∑ j β j ∣ j ⟩ |\psi\rangle = \sum_j \beta_j|j\rangle ∣ ψ ⟩ = ∑ j β j ∣ j ⟩ c i j = α i β j c_{ij} = \alpha_i \beta_j c ij = α i β j 또는 행렬 C = ( c i j ) C = (c_{ij}) C = ( c ij ) 상태가 1 2 ( ∣ a ⟩ + ∣ c ⟩ ) ⊗ ∣ b ⟩ \frac{1}{\sqrt{2}}(|a\rangle + |c\rangle) \otimes |b\rangle 2 1 ( ∣ a ⟩ + ∣ c ⟩) ⊗ ∣ b ⟩ 공통 인수를 분리할 수 있으면 product state일 가능성이 높습니다 각 선택지를 확인합니다:
결과: 선택지 A, B, D, E가 얽힌 상태입니다.
A : 계수 행렬의 rank가 1이 아니므로 product state로 표현할 수 없습니다B : 계수 행렬의 rank가 1이 아니므로 product state로 표현할 수 없습니다D : 계수 행렬의 rank가 1이 아니므로 product state로 표현할 수 없습니다E : 계수 행렬의 rank가 1이 아니므로 product state로 표현할 수 없습니다다른 선택지들은 얽힌 상태가 아닙니다 (product state):
C : 1 2 ( ∣ a ⟩ + ∣ c ⟩ ) ⊗ ∣ b ⟩ \frac{1}{\sqrt{2}}(|a\rangle + |c\rangle) \otimes |b\rangle 2 1 ( ∣ a ⟩ + ∣ c ⟩) ⊗ ∣ b ⟩ F : 명시적으로 product state 형태로 표현되어 있습니다